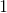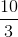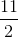How to find the slope of parallel lines
Help Questions
PSAT Math › How to find the slope of parallel lines
Which of the following lines is parallel to 
Explanation
Two lines are parallel if they have the same slope. In the 


In the xy-plane, what is the equation for a line that is parallel to 

Explanation
In order to solve the equation for this line, you need to things: the slope, and at least one point. You are already given a point for the line, so you just need to figure out the slope. The other piece of information you have is a line parallel to the line that you're looking for; since parallel lines have the same slope, you just need to figure out the slope of the parallel line you've already been given.
To figure out the slope, change the equation into point-slope form (y = m_x+_b) so the slope m is easy to find. To do that, you need to isolate y on one side of the equation.
By the calculations above, you'll find that the slope of the parallel line is -1/2.
Now, use this slope of -1/2 and the point 4,1 to find the equation. First, plug them both into the point-slope form, then solve for the slope-intercept form.
Consider line c to be y= -4x - 7. Which is the reflection of line c across the x-axis?
y = –4x + 7
y = 4x – 7
y = 4x + 7
y = (1/4)x + 7
Explanation
A line reflected across the x-axis will have the negative value of the slope and intercept. This leaves y= 4x + 7.
Line 

If line 





Explanation
We are told that lines l and m are parallel. This means that the slope of line m must be the same as the slope of l. Line l is written in the standard form of Ax + By = C, so its slope is equal to –A/B, or –2/–3, which equals 2/3. Therefore, the slope of line m must also be 2/3.
We are told that line m passes through the points (1, 4) and (2, a). The slope between these two points must equal 2/3. We can use the formula for the slope between two points and then set this equal to 2/3.

slope = (a – 4)/(2 – 1) = a – 4 = 2/3
a – 4 = 2/3
Multiply both sides by 3:
3(a – 4) = 2
3a – 12 = 2
Add 12 to both sides:
3a = 14
a = 14/3
If line J passes through the points (1, 3) and (2, 4) and line K passes through (0, x) and (10, 3), what would be the value of x in order for lines J and K to be parallel?
–7
7
1
13
–13
Explanation
Find the slope of line J, (4 – 3)/(2 – 1) = 1
Now use this slope in for the equation of line K of the form y = mx + b for the other point (10, 3)
3 = 10 + b → b = –7
So for the point (0, X) → X = 0 – 7,
so x = –7 when these two lines are parallel.