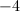How to find out when an equation has no solution
Help Questions
PSAT Math › How to find out when an equation has no solution
There is no solution
3
–3
1
–1/2
Explanation
Consider the equation
Which of the following is true?
The equation has exactly two real solutions, which are of unlike sign.
The equation has no real solutions.
The equation has exactly two real solutions, which are of like sign.
The equation has exacty one real solution, which is positive.
The equation has exacty one real solution, which is negative.
Explanation
Multiply both sides by LCD 
or
There are two solutions of unlike sign.
Consider the equation
Which of the following is true?
The equation has exactly two solutions, which are of unlike sign.
The equation has exactly two solutions, which are of like sign.
The equation has exactly one solution, which is positive.
The equation has exactly one solution, which is negative.
The equation has no solution.
Explanation
Multiply the equation on both sides by LCM 
or
Substitution confirms that these are the solutions.
There are two solutions of unlike sign.
All of the following equations have no solution except for which one?
Explanation
Since all of the equations have the same symbols save for one number, the problem is essentially as follows:
For what value of 
have a solution set other than the empty set?
We can simplify as follows:
If 



Therefore, the only equation among the given choices whose solution set is not the empty set is the equation
which is the correct choice.
Which of the following equations has no real solutions?
Each of the equations given in the other choices has at least one real solution.
Explanation
We can examine each individually.
This equation has a solution.
This equation has a solution.
This equation has a solution.
This equation has no solution, since a fourth root of a number must be nonnegative.
The correct choice is ![-14 - \sqrt[4]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234982/gif.latex)
Which of the following equations has no solution?
Each of the equations in the other responses has no solution.
Explanation
The problem is basically asking for what value of 
has no solution.
We can simplify as folllows:
Since the absolute value of a number must be nonnegative, regardless of the value of 
Solve 
No solutions
Explanation
By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.
Find the solution to the following equation if x = 3:
y = (4x2 - 2)/(9 - x2)
0
6
3
no possible solution
Explanation
Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.
None of the other answers
Explanation
A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.
I. x = 0
II. x = –1
III. x = 1
I only
II only
III only
II and III only
I, II, and III








































![-14 - \sqrt[4]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234933/gif.latex)
![-14 - \sqrt[3]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234934/gif.latex)
![14 - \sqrt[3]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234935/gif.latex)
![14 - \sqrt[4]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234936/gif.latex)
![14 - \sqrt[3]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234961/gif.latex)
![14 - \sqrt[3]{x - 7 } + 7 + \sqrt[3]{x - 7 } = -7 + 7 + \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234962/gif.latex)
![21 = \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234963/gif.latex)
![21^{3} =\left ( \sqrt[3]{x - 7 } \right )^{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234964/gif.latex)


![-14 - \sqrt[3]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234967/gif.latex)
![-14 - \sqrt[3]{x - 7 } - 7 + \sqrt[3]{x - 7 } = 7 - 7 + \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234968/gif.latex)
![-21 = \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234969/gif.latex)
![\left (-21 \right )^{3} =\left ( \sqrt[3]{x - 7 } \right )^{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234970/gif.latex)


![14 - \sqrt[4]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234973/gif.latex)
![14 - \sqrt[4]{x - 7 } + 7 + \sqrt[4]{x - 7 } = -7 + 7 + \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234974/gif.latex)
![21 = \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234975/gif.latex)
![21^{4} =\left ( \sqrt[4]{x - 7 } \right )^{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234976/gif.latex)


![-14 - \sqrt[4]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234979/gif.latex)
![-14 - \sqrt[4]{x - 7 } - 7 + \sqrt[4]{x - 7 } = 7 - 7 + \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234980/gif.latex)
![-21 = \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234981/gif.latex)