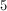How to find median
Help Questions
PSAT Math › How to find median
The number n is to be added to the list {3, 4, 5, 6, 10, 12}. If n is an integer, which of the following could be the median of the new list of seven numbers?
I) 5
II) 5.5
III) 6
I and III only
I, II, and III
I and II only
II and III only
I only
Explanation
Before n is added to the list, the median is 5.5 (the average of 5 and 6). When n is added to the list, the number of elements becomes odd, so the median will be a value directly from the list, not the average of two values. All of the values in the old list are integers and n is an integer, so the new median must be an integer; therefore, 5.5 cannot be the median of the new list.
Considering some possible values of n, we see that in cases where n is less than or equal to 5, the fourth element in the new list would be 5, making the new median 5. In cases where n is greater than or equal to 6, the fourth element in the new list would be 6, making the new median 6. The possible values for the median of the new list are therefore 5 and 6, but not 5.5.
A car travels at 60 miles per hour for 3 hours, 55 miles per hour for 2 hours, and 40 miles per hour for 3 hours. What (to the closest hundreth) is its average speed over the whole course of this trip?
51.67 miles per hour
58.13 miles per hour
55 miles per hour
19.38 miles per hour
51.25 miles per hour
Explanation
The easiest way to solve this is to find the total number of miles traveled by the car and divide that by the total time travelled.
Recall that D = rt; therefore, for each of these three periods, we can calculate the distance and sum those products:
Dtotal = 60 * 3 + 55 * 2 + 40 * 3 = 180 + 110 + 120 = 410
The total amount of time travelled is: 3 + 2 + 3 = 8
Therefore, the average rate is 410 / 8 = 51.25 miles per hour.
Find the median of the data set:
25, 37, 13, 58, 52, 83, 21, 51
44
13
83
70
42.5
Explanation
42.5 is the mean of the data. 13 is the minimum. 83 is the maximum. 70 is the range.
To find the median, list all numbers in order:
13, 21, 25, 37, 51, 52, 58, 83
and find the middle value. In cases like this where there are two middle numbers (37 and 51), find the mean of these two numbers.
(37+51)/2 = 88/2 = 44
The Brenner cousins' heights, in inches, are as follows:
Jeremy: 64
Vanessa: 69
Tracie: 60
Samuel: 70
Raymond: 74
Justin: 72
Patty: 55
Lauren: 52
Keith: 58
What is the median height of the cousins?
52
58
60
64
74
Explanation
To find the median, one must arrange all the heights from the lowest to the highest value and then pick the middle value.
All values: 64 69 60 70 74 72 55 52 58
In order from lowest: 52 55 58 60 64 69 70 72 74
Median: 64
Find the median
Explanation
To find the median, arrange the numbers from lowest to highest then find the middle number.
There are two numbers in the middle in this set (

In this case, the median is 6 but you would typically find the average of the two numbers in the middle.
Craig has a jar full of loose change. He has 20 quarters, 15 dimes, 35 nickels and 55 pennies. If he orders them all from least to most valuable, what is the value of the median coin?
Explanation
The median is the coin which has an equal number of coins of lesser or equal value and greater or equal value on either side of it. The median therefore falls to one of the nickels (62 quarters, dimes and nickels above it and 62 nickels and pennies below it). The value of a nickel is 5 cents.
The average of 5, 10, 12, 15, and x is 11. What is the median?
11
12
13
15
Explanation
You must first find what x is in order to find the median.
To find x, set up the following equation:

To solve the equation, first multiply both sides by 5:
5 + 10 + 12 + 15 + x = 55
Then, add up 5 + 10 + 12 + 15 to get 42:
42 + x = 55
x = 13
Now that you know what x is, you are ready to find the median. To find the median, order the numbers from lowest to highest. The median is the number in the middle.
5, 10, 12, 13, 15
x is the median of this set of numbers: x, 7, 12, 15, 19, 20, 8. What is one possible value of x?
14
11
17
18
16
Explanation
The median is the "middle number" in a sorted list of number; therefore, reorder the numbers in numerical order: 7, 8, 12, 15, 19, 20. Since x is the middle number, it must come between 12 and 15, leaving 14 as the only viable choice.

The monthly averaged high-and low-temperatures in Michigan are shown in the given table. What are the median monthly averaged high- and low-temperatures respectively in Michigan?
high: 56F, low: 30F
high: 60F, low: 39F
high: 58F, low: 37F
high: 46F, low: 35F
high: 56F, low: 35F
Explanation
Median is the middle number when the data are ordered from least to greatest. In this case, there are 12 numbers, so, the median is the average of the middle two numbers, which are the 6th and 7th numbers in an ascending order. For the averaged high-temperature, the median is (56+60)/2=58, and for the averaged low-temperature, the median is (35+39)/2=37
M is a set consisting of a finite number of consecutive integers. If the average (arithmetic mean) of the numbers in set M is equal to one of the numbers in set M, which of the following must be true?
I. The number of numbers in set M is odd.
II. The average (arithmetic mean) of the numbers in set M equals the median.
III. Set M has a unique mode.
I only
II only
I and II only
I and III only
I, II, and III
Explanation
Statement I must be true because if M had an even number of consecutive integers, then its average (and median) would be the average of two consecutive integers, which is a decimal value rather than an integer, and therefore cannot be in set M, which contains only integers.
To check Statement II, consider some simple possible sets for M such as {0,1,2}. We see that in a set with an odd number of items, like M, the median is always the middle element. We also see that in a set with an odd number of consecutive integers (such as {0,1,2}), the average of the set will always be the exact middle element, too. Therefore, the average and the median must be equal, and Statement II must be true.
Finally, we can find a counterexample to statement III to show that it does not have to be true. If set M is {0,1,2}, we see that there is no unique mode (in fact, the only time set M could have a unique mode is when it only has one element!)