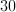Plane Geometry
Help Questions
PSAT Math › Plane Geometry
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
2√5
11
10√2
15
6√2
Explanation
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c

Refer to the above diagram. 
Give the area of Quadrilateral 
Explanation



By the Angle-Angle Similarity Postulate, since
and


and since corresponding sides of similar triangles are in proportion,

The smaller base is 

The area of the trapezoid is
All of the following could be the possible side lengths of a triangle EXCEPT:
Explanation
The length of the third side of a triangle must always be between (but not equal to) the sum and the difference of the other two sides.
For instance, take the example of 2, 6, and 7.


The 5, 7, 12 answer choice is the only option for which this is not the case.



Note: Figure NOT drawn to scale.
The above figure shows Rectangle 




What percent of Rectangle 
Explanation
The area of 


The answer is independent of the sidelengths of the rectangle, so to ease calculations - this will become more apparent later - we will arbitrarily assign to the rectangle the dimensions
and, subsequently,
and, since 


The area of Rectangle 

Since 


The area of 

The area of 
The area of the shaded region is therefore 

What is the area of a square that has a diagonal whose endpoints in the coordinate plane are located at (-8, 6) and (2, -4)?
100
100√2
50√2
50
200√2
Explanation
The base angle of an isosceles triangle is 15 less than three times the vertex angle. What is the vertex angle?
Explanation
Every triangle contains 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

So the equation to solve becomes 
A square with a side length of 4 inches is inscribed in a circle, as shown below. What is the area of the unshaded region inside of the circle, in square inches?

8π - 16
4π-4
8π-4
2π-4
8π-8
Explanation
Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2. Thus, the radius of the circle is half of the diameter, or 2√2. The area of the circle is then π(2√2)2, which equals 8π. Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.
100_π_
50_π_
25_π_
10_π_
20_π_
Explanation
100_π_
50_π_
25_π_
10_π_
20_π_
Explanation
A square with a side length of 4 inches is inscribed in a circle, as shown below. What is the area of the unshaded region inside of the circle, in square inches?

8π - 16
4π-4
8π-4
2π-4
8π-8
Explanation
Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2. Thus, the radius of the circle is half of the diameter, or 2√2. The area of the circle is then π(2√2)2, which equals 8π. Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.