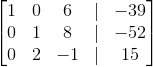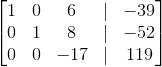Solve a System of Equations in Three Variables Using Augmented Matrices
Help Questions
Pre-Calculus › Solve a System of Equations in Three Variables Using Augmented Matrices
Determine which 
Explanation
The system of equations in matrix form is written:
Beginning with the top equation, insert each coefficient into the top row of the matrix, from left to right. Then, place the 2 on the right hand side of the vertical line (anytime you see this vertical line in a matrix, it is called an augmented matrix. Because the first equation's coefficients are 1, 1, and 1, these form the top row of the matrix, with 2 on the right side of the bar. Then, move on to the second row, which has coefficients 2, -1, and 3. Place these into the second row of the matrix, with -7 on the right hand side of the vertical bar. Finally, take the coefficients from the 3rd equation, 1, 1, and -1, and place these in the bottom row with 6 on the right hand side of the vertical bar.
True or false: there is no solution 
False
True
Explanation
For two matrices to be equal, two conditions must hold:
-
The matrices must have the same dimension. This can be seen to be the case, since both matrices have two rows and one column.
-
All corresponding entries must be equal. For this to happen, it must hold that
This is a system of two equations in two variables, which can be solved as follows:
Add both sides of the equations:
It follows that
Substitute back:
Thus, there exists a solution to the system, and, consequently, to the original matrix equation. The statement is therefore false.
Express this system of equations as an augmented matrix:
Explanation
Arrange the equations into the form:

Then we have the system of equations: 
The augmented matrix is found by copying the constants into the respective rows and columns of a matrix.
The vertical line in the matrix is analogous to the = sign thus resulting in the following:


True or false: 

True
False
Explanation
First, it must be established that 



Addition of two matrices is performed by adding corresponding elements, so
This is the two-by-two identity 

Using an augmented matrix, solve the following system of equations:
Which of the following are the values of 


Explanation
Create an augmented matrix by entering the coefficients into one matrix and appending a vector to that matrix with the constants that the equations are equal to. Then you can row reduce to solve the system.
First, lets make this augmented matrix:
Now we can row reduce the matrix using the three row reduction operations: mutliply a row, add one row to another, swap row positions.
First, we can subtract 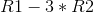
Swap
Subtract
Add
Subtract
Mulitply
You can stop here given that this augmented matrix can be rewritten as a system again with


Using the Reduced Row Echelon Method, the solution matrix to the system of equations reads

Which of the following is the accurate depiction of this matrix?
Explanation
Traditionally in Row Reduced Echelon Form (first row's values are 1,0,0; second row's values are 0,1,0; third row's values are 0,0,1), x is depicted in the first row, 





![\left[\begin{array}{ccc|c} 1 & 0 & 0 & 2\ 0 & 1 & 0 & -7\ 0 & 0 & 1 & 6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172866/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 2\ 2 & -1 & 3 & -7\ 1 & 1 & -1 & 6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172867/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 0\ 2 & -1 & 3 & 0\ 1 & 1 & -1 & 0 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172868/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 1\ 2 & -1 & 3 & 1\ 1 & 1 & -1 & 1 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172869/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & -2\ 2 & -1 & 3 & 7\ 1 & 1 & -1 & -6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172870/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 2\ 2 & -1 & 3 & -7\ 1 & 1 & -1 & 6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172871/gif.latex)








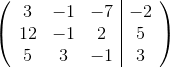



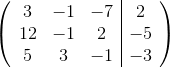






![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & 3&\left | -7 \right | \ 1& 1& -1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175146/gif.latex)
![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & 3&\left | 7 \right | \ 1& 1& 1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175147/gif.latex)
![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & -3&\left | 7 \right | \ 1& 1& -1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175148/gif.latex)
![\left [ \begin{bmatrix} 2 & 1& 1& \left | 1 \right |\ 2& -1 & 3&\left | -7 \right | \ 6& -1& 1 & \left | 1 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175149/gif.latex)
![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & 3&\left | -7 \right | \ 1& 1& -1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175153/gif.latex)