Augmented Matrices
Help Questions
Pre-Calculus › Augmented Matrices
Determine which 
Explanation
The system of equations in matrix form is written:
Beginning with the top equation, insert each coefficient into the top row of the matrix, from left to right. Then, place the 2 on the right hand side of the vertical line (anytime you see this vertical line in a matrix, it is called an augmented matrix. Because the first equation's coefficients are 1, 1, and 1, these form the top row of the matrix, with 2 on the right side of the bar. Then, move on to the second row, which has coefficients 2, -1, and 3. Place these into the second row of the matrix, with -7 on the right hand side of the vertical bar. Finally, take the coefficients from the 3rd equation, 1, 1, and -1, and place these in the bottom row with 6 on the right hand side of the vertical bar.
Determine which 
Explanation
The system of equations in matrix form is written:
Beginning with the top equation, insert each coefficient into the top row of the matrix, from left to right. Then, place the 2 on the right hand side of the vertical line (anytime you see this vertical line in a matrix, it is called an augmented matrix. Because the first equation's coefficients are 1, 1, and 1, these form the top row of the matrix, with 2 on the right side of the bar. Then, move on to the second row, which has coefficients 2, -1, and 3. Place these into the second row of the matrix, with -7 on the right hand side of the vertical bar. Finally, take the coefficients from the 3rd equation, 1, 1, and -1, and place these in the bottom row with 6 on the right hand side of the vertical bar.
True or false: there is no solution 
False
True
Explanation
For two matrices to be equal, two conditions must hold:
-
The matrices must have the same dimension. This can be seen to be the case, since both matrices have two rows and one column.
-
All corresponding entries must be equal. For this to happen, it must hold that
This is a system of two equations in two variables, which can be solved as follows:
Add both sides of the equations:
It follows that
Substitute back:
Thus, there exists a solution to the system, and, consequently, to the original matrix equation. The statement is therefore false.
True or false: there is no solution 
False
True
Explanation
For two matrices to be equal, two conditions must hold:
-
The matrices must have the same dimension. This can be seen to be the case, since both matrices have two rows and one column.
-
All corresponding entries must be equal. For this to happen, it must hold that
This is a system of two equations in two variables, which can be solved as follows:
Add both sides of the equations:
It follows that
Substitute back:
Thus, there exists a solution to the system, and, consequently, to the original matrix equation. The statement is therefore false.
Express this system of equations as an augmented matrix:
Explanation
Arrange the equations into the form:

Then we have the system of equations: 
The augmented matrix is found by copying the constants into the respective rows and columns of a matrix.
The vertical line in the matrix is analogous to the = sign thus resulting in the following:


True or false: 

True
False
Explanation
First, it must be established that 



Addition of two matrices is performed by adding corresponding elements, so
This is the two-by-two identity 

Express this system of equations as an augmented matrix:
Explanation
Arrange the equations into the form:

Then we have the system of equations: 
The augmented matrix is found by copying the constants into the respective rows and columns of a matrix.
The vertical line in the matrix is analogous to the = sign thus resulting in the following:


True or false: 

True
False
Explanation
First, it must be established that 



Addition of two matrices is performed by adding corresponding elements, so
This is the two-by-two identity 




![\left[\begin{array}{ccc|c} 1 & 0 & 0 & 2\ 0 & 1 & 0 & -7\ 0 & 0 & 1 & 6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172866/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 2\ 2 & -1 & 3 & -7\ 1 & 1 & -1 & 6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172867/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 0\ 2 & -1 & 3 & 0\ 1 & 1 & -1 & 0 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172868/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 1\ 2 & -1 & 3 & 1\ 1 & 1 & -1 & 1 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172869/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & -2\ 2 & -1 & 3 & 7\ 1 & 1 & -1 & -6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172870/gif.latex)
![\left[\begin{array}{ccc|c} 1 & 1 & 1 & 2\ 2 & -1 & 3 & -7\ 1 & 1 & -1 & 6 \end{array}\right]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172871/gif.latex)








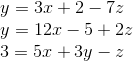
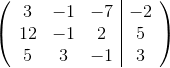



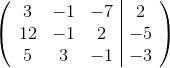






![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & 3&\left | -7 \right | \ 1& 1& -1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175146/gif.latex)
![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & 3&\left | 7 \right | \ 1& 1& 1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175147/gif.latex)
![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & -3&\left | 7 \right | \ 1& 1& -1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175148/gif.latex)
![\left [ \begin{bmatrix} 2 & 1& 1& \left | 1 \right |\ 2& -1 & 3&\left | -7 \right | \ 6& -1& 1 & \left | 1 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175149/gif.latex)
![\left [ \begin{bmatrix} 1 & 1& 1& \left | 2 \right |\ 2& -1 & 3&\left | -7 \right | \ 1& 1& -1 & \left | 6 \right | \end{bmatrix} \right ]](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1175153/gif.latex)