Graphing Tangent, Cosecant, Secant, and Cotangent Functions
Help Questions
Pre-Calculus › Graphing Tangent, Cosecant, Secant, and Cotangent Functions
Which of the following represents the asymptotes for the general parent function 
Explanation
If you do not have these asymptotes memorized, they can be easily derived. Write 

Now we need to solve for 





Which of the following represents the asymptotes for the general parent function 
Explanation
If you do not have these asymptotes memorized, they can be easily derived. Write 

Now we need to solve for 





Find the vertical asymptote of the equation.
There are no vertical asymptotes.
Explanation
To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.
True or false: There is a vertical asymptote for 
The statement is true.
The statement is false.
There is insufficient information to answer the question.
Explanation
We know that the parent function of 






So when 

Given the function 

Assume that there is a vertical asymptote for the function 



Explanation
We know that the parent function 


Now we will add this to the parent function equation for vertical asymptotes
Now we will set this equation for the given vertical asymptote at
True or false: There is a vertical asymptote for 
The statement is true.
The statement is false.
There is insufficient information to answer the question.
Explanation
We know that the parent function of 






So when 

Find the vertical asymptote of the equation.
There are no vertical asymptotes.
Explanation
To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.
Given the function 

Assume that there is a vertical asymptote for the function 



Explanation
We know that the parent function 


Now we will add this to the parent function equation for vertical asymptotes
Now we will set this equation for the given vertical asymptote at






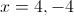















 has vertical asymptotes at
has vertical asymptotes at  where
where  is any integer. We will set the quantity inside the
is any integer. We will set the quantity inside the  function equal to zero to solve for the shift of the asymptote.
function equal to zero to solve for the shift of the asymptote.














