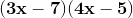Graphing Functions
Help Questions
Pre-Calculus › Graphing Functions
Which of the following equations could represent a cosine function with amplitude 3, period 

Explanation
The form of the equation will be
First, think about all possible values of A that could give you an amplitude of 3. Either A = -3 or A = 3 could each produce amplitude = 3. Be sure to look for answer choices that satisfy either of these.
Secondly, we know that the period is 

Finally, we need to find a value of C that satisfies


Next, plug in B= 4 to solve for C:
Putting this all together, the equation could either be:

Solve this polynomial by factoring if it is factorable:
Not factorable
Explanation
To factor this polynomial it is prudent to recognize that there will only be two factors since the highest power is 
Then ask what numbers multiply to equal postive 35.
Next, what numbers can multiply to equal positive 12.
Let's try 7 and 5 for the last term and 3 and 4 for the first term.
Be sure to put an "x" in the first term of each factor.
Choose the signs based on what the polynomial calls for. In our case we choose negative signs to get positive 35.
Foil these two factors and we get 
Solve the following polynomial for 
Explanation
The polynomial in the problem is given as follows:
Factoring this polynomial, we would get an expression of the form:
So we need to determine what a and b are. We know we need two factors that when multiplied equal -12, and when added equal -1. If we consider 2 and 6, we could get -12 but could not arrange them in any way that would make their sum equal to -1. We then look at 3 and 4, whose product can be -12 is one of them is negative, and whose sum can be -1 if -4 is added to 3. This tells us that the 4 must be the negative factor and the 3 must be the positive factor, so we get the following:
True or false: for a quadratic function of form ax2 + bx + c = 0, if the discriminant b2 - 4ac = 0, there is exactly one real root.
True
False
Explanation
This is true. The discriminant b2 - 4ac is the part of the quadratic formula that lives inside of a square root function. As you plug in the constants a, b, and c into b2 - 4ac and evaluate, three cases can happen:
b2 - 4ac > 0
b2 - 4ac = 0
b2 - 4ac < 0
In the first case, having a positive number under a square root function will yield a result that is a positive number answer. However, because the quadratic function includes 
In the middle case (the case of our example), 


For the final case, if b2 - 4ac < 0, that means you have a negative number under a square root. This means that you will not have any real roots of the equation; however, you will have exactly two imaginary roots of the equation.
Is the following function symmetrical about the y axis (is it an even function)?
Yes
No
Insufficient Information
Not a function
Explanation
For a function to be even, it must satisfy the equality
Likewise if a function is even, it is symmetrical about the y-axis
Therefore, the function is not even, and so the answer is No
Find the zeros of the function 
Explanation
To find the zeros of the function, you need to factor the equation. Using trial and error, you should arrive at: 


Solve this polynomial by factoring if it is factorable:
Not factorable
Explanation
To factor this polynomial it is prudent to recognize that there will only be two factors since the highest power is 
Then ask what numbers multiply to equal postive 35.
Next, what numbers can multiply to equal positive 12.
Let's try 7 and 5 for the last term and 3 and 4 for the first term.
Be sure to put an "x" in the first term of each factor.
Choose the signs based on what the polynomial calls for. In our case we choose negative signs to get positive 35.
Foil these two factors and we get 
Solve the following polynomial for 
Explanation
The polynomial in the problem is given as follows:
Factoring this polynomial, we would get an expression of the form:
So we need to determine what a and b are. We know we need two factors that when multiplied equal -12, and when added equal -1. If we consider 2 and 6, we could get -12 but could not arrange them in any way that would make their sum equal to -1. We then look at 3 and 4, whose product can be -12 is one of them is negative, and whose sum can be -1 if -4 is added to 3. This tells us that the 4 must be the negative factor and the 3 must be the positive factor, so we get the following:
Find the distance from point 

Explanation
Draw a line that connects the point and intersects the line at a perpendicular angle.
The vertical distance from the point 

The distance can never be negative.
Which of the following functions is represented by this graph?

y = sin(x)
y = cos(x)
y = tan(x)
y = sec(x)
y = csc(x)
Explanation
This graph is the graph of y = cos x. The domain of this function is all real numbers. The range of this function is