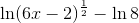Exponential and Logarithmic Functions
Help Questions
Pre-Calculus › Exponential and Logarithmic Functions
Solve:
None of the other answers.
Explanation
Combine the constants:
Isolate the exponential function by dividing:
Take the natural log of both sides:
Finally isolate x:
Solve for 
Explanation
First, let's begin by simplifying the left hand side.







Now, our expression is
From this, we can cancel out the 2's and an x from both sides.
Thus our answer becomes:

Solve for 
Explanation
First, let's begin by simplifying the left hand side.







Now, our expression is
From this, we can cancel out the 2's and an x from both sides.
Thus our answer becomes:

Solve:
None of the other answers.
Explanation
Combine the constants:
Isolate the exponential function by dividing:
Take the natural log of both sides:
Finally isolate x:
Solve for 
Explanation
First, let's begin by simplifying the left hand side.







Now, our expression is
From this, we can cancel out the 2's and an x from both sides.
Thus our answer becomes:

Solve:
None of the other answers.
Explanation
Combine the constants:
Isolate the exponential function by dividing:
Take the natural log of both sides:
Finally isolate x:
Solve the equation for 
Explanation
The key to this is that 




Now take the natural log (ln) of the two equations.


Solve the equation for 
Explanation
The key to this is that 




Now take the natural log (ln) of the two equations.


Solve the equation for 
Explanation
The key to this is that 




Now take the natural log (ln) of the two equations.


Completely expand this logarithm:
The answer is not present.
Explanation
We expand logarithms using the same rules that we use to condense them.
Here we will use the quotient property
and the power property
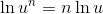
Use the quotient property:
Rewrite the radical:
Now use the power property: