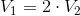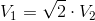SSAT Upper Level Quantitative - How to find the volume of a cylinder

The height of a cylinder is 3 inches and the radius of the circular end of the cylinder is 3 inches. Give the volume and surface area of the cylinder.

Explanation

The volume of a cylinder is found by multiplying the area of one end of the cylinder (base) by its height or:

$Volume=\pi r^2h$

where is the radius of the circular end of the cylinder and is the height of the cylinder. So we can write:

$Volume=\pi r^2h=\pi \times 3^2\times 3=84.82in^3$

The surface area of the cylinder is given by:

$A=2\pi r^2+2\pi rh$

where is the surface area of the cylinder, is the radius of the cylinder and is the height of the cylinder. So we can write:

$A=2\pi r^2+2\pi rh$

$A=2\pi (3)^2+2\pi \times 3\times 3$

$A=18\pi+18\pi$

$A=36\pi$

The height of a cylinder is two times the length of the radius of the circular end of a cylinder. If the volume of the cylinder is $16\pi$ , what is the height of the cylinder?

$2\sqrt{2}$

Explanation

The volume of a cylinder is:

$Volume=\pi r^2h$

where is the radius of the circular end of the cylinder and is the height of the cylinder.

Since , we can substitute that into the volume formula. So we can write:

$Volume=\pi r^2h$

$16\pi=\pi r^2\cdot (2r)$

$16\pi =2\pi r^{3}$

$16=2r^{3}$

$8=r^{3}$

So we get:

$h=2r=2\times 2=4$

We have two right cylinders. The radius of the base Cylinder 1 is $\sqrt{3}$ times more than that of Cylinder 2, and the height of Cylinder 2 is 4 times more than the height of Cylinder 1. The volume of Cylinder 1 is what fraction of the volume of Cylinder 2?

$V_{1}=\frac{3}{4}V_{2}$

$V_{1}=\frac{4}{3}V_{2}$

$V_{1}=V_{2}$

$V_{1}=\frac{2}{3}V_{2}$

$V_{1}=\frac{3}{2}V_{2}$

Explanation

The volume of a cylinder is:

$V=\pi r^2h$

where is the volume of the cylinder, is the radius of the circular end of the cylinder, and is the height of the cylinder.

So we can write:

$V_{1}=\pi (r_{1})^2h_{1}$

and

$V_{2}=\pi (r_{2})^2h_{2}$

Now we can summarize the given information:

$r_{1}=\sqrt{3}\cdot r_{2}$

$h_{2}=4\cdot h_{1}\Rightarrow h_{1}=\frac{h_{2}}{4}$

Now substitute them in the $V_{1}$ formula:

$V_{1}=\pi (\sqrt{3}r_{2})^2\times \frac{h_{2}}{4}\Rightarrow V_{1}=\frac{3}{4}\pi (r_{2})^2\times h_{2}\Rightarrow V_{1}=\frac{3}{4}V_{2}$

The end (base) of a cylinder has an area of $16\pi$ square inches. If the height of the cylinder is half of the radius of the base of the cylinder, give the volume of the cylinder.

$32\pi$

$16\pi$

$8\pi$

Explanation

The area of the end (base) of a cylinder is $\pi r^2$ , so we can write:

$\pi r^2=16\pi\Rightarrow r^2=16\Rightarrow r=4\ inches$

The height of the cylinder is half of the radius of the base of the cylinder, that means:

$h=\frac{r}{2}=\frac{4}{2}=2\ inches$

The volume of a cylinder is found by multiplying the area of one end of the cylinder (base) by its height:

$Volume=Area\times h=16\pi\times 2=32\pi$

$Volume=\pi r^2h=\pi\times 4^2\times 2=32\pi$

Two right cylinders have the same height. The radius of the base of the first cylinder is two times more than that of the second cylinder. Compare the volume of the two cylinders.

$V_{1}=4\cdot V_{2}$