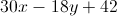How to multiply variables
Help Questions
SSAT Middle Level Quantitative › How to multiply variables
Which of the following is NOT the same as
Explanation
The answer shows that the 3 in front of the 

Solve the following expression,

The expression is already solved.
Explanation
When multiplying like variables, the constants are multiplied together.
For the exponents, when you multply variable exponents you have to add the exponents together.



Simplify:
Explanation
Apply the distributive property:
Multiply in modulo 8:
None of the other choices give the correct answer.
Explanation
In modulo 8 arithmetic, a number is congruent to the remainder of the divison of that number by 8. Since
and
then

The correct response is 4.
Suppose you know the values of all variables in the expression
and you want to evaluate the expression.
In which order will you carry out the operations?
Adding, squaring, multiplying
Squaring, multiplying, adding
Multiplying, adding, squaring
Multiplying, squaring, adding
Adding, multiplying, squaring
Explanation
By the order of operations, the operation inside grouping symbols, which here is addition, takes precendence, followed by, in order, squaring and multiplication.
Which of the following phrases can be written as the algebraic expression 
Fifty-five subtracted from the product of nine and a number
The product of nine and a number subtracted from fifty-five
Nine multiplied by the difference of a number and fifty-five
Nine multiplied by the difference of fifty-five and a number
The correct answer is not given among the other responses.
Explanation



Subsequently, 
Simplify:
Explanation
To solve, you can use the commutative and associative properties of multiplication to group like-terms together.
The 4 and 3 should be first multiplied, resulting in 12.
Next 


12 times 

Therefore, the correct answer is 
Given 



Explanation


Simplify:
Explanation
Apply the distributive property:
Simplify:
Explanation
Apply the distributive property: