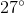SAT Math - Finding Angles with Trigonometry

What is the measure of the angle made between a line segment with points , and the -axis? Round your answer to the nearest hundreth of a degree.

$58.00^{\circ}$

$82.87^{\circ}$

$71.42{^{\circ}}$

$12.42^{\circ}$

No angle measure can be calculated

Explanation

Based on the information given, we know that the ratio of to on this segment could be represented as:

$\frac{8}{5}$

This ratio represents the tangent of the triangle formed by our line segment and the -axis. Using the inverse tangent function, we can find the angle measure:

$\tan^{-1}(\frac{8}{5}) = 57.9946167919165$

This refers to a reference angle of $58.00^{\circ}$

A triangle is formed by connecting the points $(0,0), (1,0), \textup{ and }(1,6)$ . Determine the elevation angle to the nearest integer in degrees.

Explanation

After connecting the points on the graph, the length of the triangular base is 1 unit.

The height of the triangle is 6. To find the elevation angle, the angle is opposite from the height of the triangle. Since we know the base and the height, the elevation angle can be solved by using the property of tangent.

$tan(\theta)= \frac{\textup{Opposite side}}{\textup{Adjacent side}}$

$tan(\theta)= \frac{\textup{6}}{\textup{1}}$

$\theta = tan^{-1}(6)=80.53768 \textup{ degrees}$

The best answer is .

In $\bigtriangleup ABC$ :

Evaluate $m \angle A$ to the nearest degree.

$47^{\circ }$

$43^{\circ }$

$90^{\circ }$

$27^{\circ }$

$63^{\circ }$

Explanation

The figure referenced is below:

Triangle z

By the Law of Cosines, the relationship of the measure of an angle $\gamma$ of a triangle and the three side lengths , , and , the sidelength opposite the aforementioned angle, is as follows:

$c^{2} = a ^{2} + b^{2} - 2ab \cos \gamma$

All three side lengths are known, so we are solving for $\gamma$ . Setting

, the length of the side opposite the unknown angle;

;

and $\gamma = \cos A$ ,

We get the equation

$25^{2} =23^{2} +34^{2} - 2 (23) (34)\cos A$

$625 =529+1,156- 1,564 \cos A$

$625 =1,685 - 1,564 \cos A$

Solving for $\cos A$ :

$625 - 1,685 =1,685 - 1,564 \cos A - 1,685$

$-1.060 = - 1,564 \cos A$

$\frac{-1.060 }{- 1,564}= \frac{- 1,564 \cos A}{- 1,564}$

$\cos A \approx 0.6777$

Taking the inverse cosine:

$A = \cos ^{-1} 0.6777 \approx 47 ^{\circ }$ ,

the correct response.

What is the measure of the angle made between a line segment with points , and the -axis? Round your answer to the nearest hundreth of a degree.

$48.81^{\circ}$

$-48.81^{\circ}$

$71.41^{\circ}$

$41.10^{\circ}$

No angle can be calculated

Explanation

Based on the information given, we know that the ratio of to on this segment could be represented as:

$\frac{-8}{7}$

This ratio represents the tangent of the triangle formed by our line segment and the -axis. Using the inverse tangent function, we can find the angle measure:

$\tan^{-1}(\frac{-8}{7}) = -48.81407483429027$

This refers to a reference angle of $48.81^{\circ}$ .

Finding Angles with Trigonometry

Help Questions

Explanation

Explanation

Explanation

Explanation