How to find the length of the side of a right triangle - ISEE Upper Level Quantitative Reasoning

Card 0 of 56

Question

Refer to the above right triangle. Which of the following is equal to ?

Answer

By the Pythagorean Theorem,

$x^{2 } + 12 ^{2 } = 18 ^{2 }$

$x^{2 } + 144 = 324$

$x^{2 } + 144 -144 = 324-144$

$x^{2 } = 180$

$x = \sqrt{180} = \sqrt{36} \cdot \sqrt{5} = 6 \sqrt{5}$

Compare your answer with the correct one above

Question

Given $\Delta ABC$ with right angle $\angle B$ , $m \angle C = 45 ^{\circ }$

Which is the greater quantity?

(a)

(b)

Answer

$m \angle B = 90^{\circ}$

$m \angle C = 45 ^{\circ }$

The sum of the measures of the angles of a triangle is , so:

$m \angle A + m \angle B + m \angle C = 180$

$m \angle A +90 + 45 = 180$

$m \angle A +135= 180$

$m \angle A +135-135= 180-135$

$m \angle A = 45^{\circ }$

This is a $45^{\circ }-45^{\circ }-90^{\circ }$ triangle, so its legs $\overline{AB}$ and $\overline{BC}$ are congruent. The quantities are equal.

Compare your answer with the correct one above

Question

Give the length of one leg of an isosceles right triangle whose area is the same as the right triangle in the above diagram.

Answer

The area of a triangle is half the product of its height and its base; in a right triangle, the legs, being perpendicular, can serve as these quantites.

The triangle in the diagram has area

$\frac{1}{2} \times 30 \times 18 = 270$ square inches.

An isosceles right triangle has two legs of the same length, which we will call . The area of that triangle, which is the same as that of the one in the diagram, is therefore

$\frac{1}{2} L ^{2} = 270$

$\frac{1}{2} L ^{2}\cdot 2 = 270 \cdot 2$

$L ^{2} = 540$

$L = \sqrt{540}$

$L = \sqrt{36}\cdot \sqrt{15} = 6 \sqrt{15}$ inches.

Compare your answer with the correct one above

Question

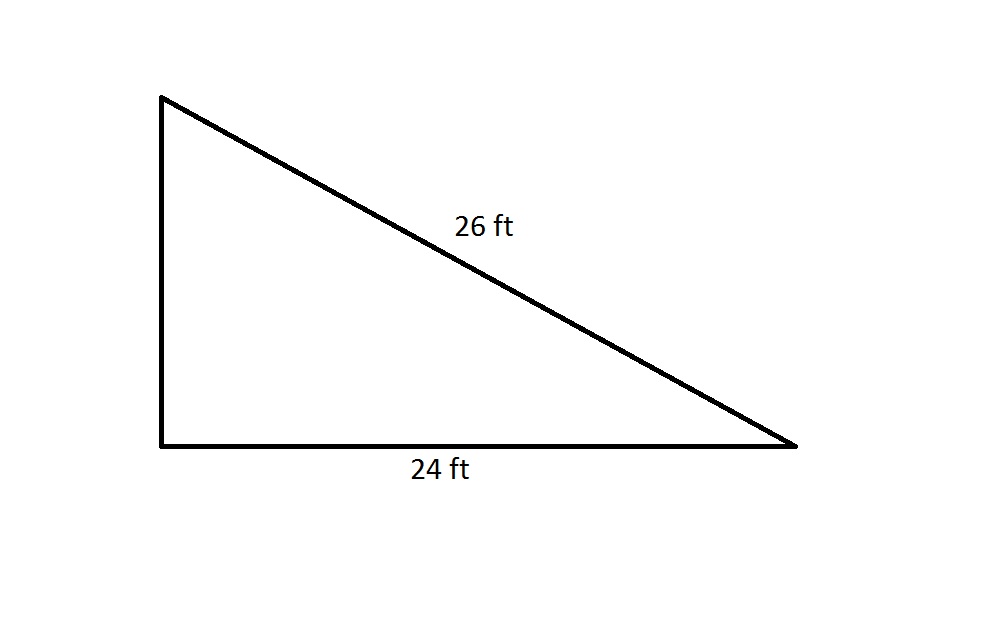
The perimeter of a regular octagon is 20% greater than that of the above right triangle. Which is the greater quantity?

(A) The length of one side of the octagon

(B) 3 yards

Answer

By the Pythagorean Theorem, the shorter leg has length

$\sqrt{26^{2}-24^{2}} = \sqrt{676-576} = \sqrt{100} = 10$ feet.

The perimeter of the right triangle is therefore

feet.

The octagon has perimeter 20% greater than this, or

$60 + 0.20 \times 60 = 60 + 12 = 72$ feet.

A regular octagon has eight sides of equal length, so each side of this octagon has length

$72 \div 8 = 9$ feet, which is equal to 3 yards. This makes the quantities equal.

Compare your answer with the correct one above

Question

The area of a square is equal to that of the above right triangle. Which is the greater quantity?

(A) The sidelength of the square

(B) 4 yards

Answer

By the Pythagorean Theorem, the shorter leg has length

$\sqrt{26^{2}-24^{2}} = \sqrt{676-576} = \sqrt{100} = 10$ feet.

The area of a triangle is equal to half the product of its base and height; for a right triangle, the legs can serve as these. The area of the above right triangle is

$\frac{1}{2} \times 10 \times 24 = 120$ square feet.

The sidelength is the square root of this; , so $\sqrt{120} < \sqrt{121} = 11$ . Therefore each sidelength of the square is just under 11 feet. 4 yards is 12 feet, so (B) is greater.

Compare your answer with the correct one above

Question

Consider a triangle, $\bigtriangleup ABC$ , in which , , and $m \angle B = 100 ^{\circ}$ . Which is the greater quantity?

(a) 55

(b)

Answer

Suppose .

By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities $(AB)^{2}+ ( BC )^{2}$ and $(AC)^{2}$

$(AB)^{2}+ ( BC )^{2} = 33^{2} + 44 ^{2} = 1,089+ 1,936= 3,025$

$(AC)^{2} = 55^{2} = 3,025$

Therefore, if

$(AB)^{2}+ ( BC )^{2} =(AC)^{2}$ , so $\bigtriangleup ABC$ is right, with the right angle opposite longest side $\overline{AC}$ . Thus, $\angle B$ is right and has degree measure 90.

However, $\angle B$ has degree measure greater than 90, so, as a consequence of the Converse of the Pythagorean Theorem and the SAS Inequality Theorem, it holds that .

Compare your answer with the correct one above

Question

Figure NOT drawn to scale.

Refer to the above triangle. Which is the greater quantity?

(a)

(b) 108

Answer

We can compare these numbers by comparing their squares.

By the Pythagorean Theorem,

$(AC) ^{2}= (AB) ^{2}+ (BC)^{2} = 100 ^{2}+ 40 ^{2} = 10,000 + 1,600 = 11,600$

Also,

$108^{2} = 11,664$

$108^{2} >(AC) ^{2}$ , so .

Compare your answer with the correct one above

Question

A right triangle has a hypotenuse of 10 and a side of 6. What is the missing side?

Answer

To find the missing side, use the Pythagorean Theorem . Plug in (remember c is always the hypotenuse!) so that . Simplify and you get Subtract 36 from both sides so that you get Take the square root of both sides. B is 8.

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram.

Find the length of $\overline{BC}$ .

Answer

First, find .

Since $\overline{DF }$ is an altitude of right $\Delta ADB$ to its hypotenuse,

$\frac{FB}{FD}= \frac{FD}{AF}$

$\frac{FB}{8}= \frac{8}{6}$

$FB= \frac{8}{6} \cdot 8 = 10 \frac{2}{3}$

$AB = AF + FB = 6 + 10 \frac{2}{3} = 16 \frac{2}{3}$

$\Delta AFD \sim \Delta ABC$ by the Angle-Angle Postulate, so

$\frac{BC}{FD} = \frac{AB}{AF}$

$\frac{BC}{8} = \frac{16 \frac{2}{3}}{6}$

$BC = 16 \frac{2}{3}\cdot 8 \div 6 = 22\frac{2}{9}$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram.

Find the length of $\overline{AB}$ .

Answer

First, find .

Since $\overline{DE}$ is an altitude of $\Delta CDB$ from its right angle to its hypotenuse,

$\Delta DEC \sim \Delta BED$

$\frac{BE}{DE}= \frac{ED}{EC}$

$\frac{BE}{6}= \frac{6}{12}$

$BE= \frac{6}{12} \cdot 6 = 3$

$\Delta DEC \sim \Delta ABC$ by the Angle-Angle Postulate, so

$\frac{AB}{DE} = \frac{CB}{CE}$

$\frac{AB}{6} = \frac{15}{12}$

$AB= \frac{15}{12} \cdot 6$

$AB = 7\frac{1}{2}$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram. Evaluate .

Answer

By the Pythagorean Theorem,

$x^{2}+ 15^{2} = (x+12)^{2}$

$x^{2}+ 225 = x^{2}+24x+144$

$x= 3\frac{3}{8}$

Compare your answer with the correct one above

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram. Which of the following quadratic equations would yield the value of as a solution?

Answer

By the Pythagorean Theorem,

$x^{2}+ (x+5)^{2} = (x+7)^{2}$

$x^{2}+ x^{2} +10x+25 = x^{2} +14x +49$

$2x^{2} +10x+25 = x^{2} +14x +49$

$x^{2} -4x-24= 0$

Compare your answer with the correct one above

Question

Refer to the above diagram. Which of the following quadratic equations would yield the value of as a solution?

Answer

By the Pythagorean Theorem,

$x^{2}+ (x+3)^{2} = 20^{2}$

$x^{2}+ x^{2}+6x+9= 400$

$2x^{2}+6x-391 = 0$

Compare your answer with the correct one above

Question

A right triangle $\Delta ABC$ with hypotenuse $\overline{AC}$ is inscribed in $\odot O$ , a circle with radius 26. If , evaluate the length of $\overline{BC}$ .

Answer

The arcs intercepted by a right angle are both semicircles, so hypotenuse $\overline{AC}$ shares its endpoints with two semicircles. This makes $\overline{AC}$ a diameter of the circle, and $AC = 2r = 2 \cdot 26 = 52$ .

By the Pythagorean Theorem,

$BC = \sqrt{(AC)^{2} - (AB)^{2}} = \sqrt{52^{2} -20^{2}} = \sqrt{2,704-400} = \sqrt{2,304} = 48$

Compare your answer with the correct one above

Question

Refer to the above right triangle. Which of the following is equal to ?

Answer

By the Pythagorean Theorem,

$x^{2 } + 12 ^{2 } = 18 ^{2 }$

$x^{2 } + 144 = 324$

$x^{2 } + 144 -144 = 324-144$

$x^{2 } = 180$

$x = \sqrt{180} = \sqrt{36} \cdot \sqrt{5} = 6 \sqrt{5}$

Compare your answer with the correct one above

Question

Given $\Delta ABC$ with right angle $\angle B$ , $m \angle C = 45 ^{\circ }$

Which is the greater quantity?

(a)

(b)

Answer

$m \angle B = 90^{\circ}$

$m \angle C = 45 ^{\circ }$

The sum of the measures of the angles of a triangle is , so:

$m \angle A + m \angle B + m \angle C = 180$

$m \angle A +90 + 45 = 180$

$m \angle A +135= 180$

$m \angle A +135-135= 180-135$

$m \angle A = 45^{\circ }$

This is a $45^{\circ }-45^{\circ }-90^{\circ }$ triangle, so its legs $\overline{AB}$ and $\overline{BC}$ are congruent. The quantities are equal.

Compare your answer with the correct one above

Question

Give the length of one leg of an isosceles right triangle whose area is the same as the right triangle in the above diagram.

Answer

The area of a triangle is half the product of its height and its base; in a right triangle, the legs, being perpendicular, can serve as these quantites.

The triangle in the diagram has area

$\frac{1}{2} \times 30 \times 18 = 270$ square inches.

An isosceles right triangle has two legs of the same length, which we will call . The area of that triangle, which is the same as that of the one in the diagram, is therefore

$\frac{1}{2} L ^{2} = 270$

$\frac{1}{2} L ^{2}\cdot 2 = 270 \cdot 2$

$L ^{2} = 540$

$L = \sqrt{540}$

$L = \sqrt{36}\cdot \sqrt{15} = 6 \sqrt{15}$ inches.

Compare your answer with the correct one above

Question

The perimeter of a regular octagon is 20% greater than that of the above right triangle. Which is the greater quantity?

(A) The length of one side of the octagon

(B) 3 yards

Answer

By the Pythagorean Theorem, the shorter leg has length

$\sqrt{26^{2}-24^{2}} = \sqrt{676-576} = \sqrt{100} = 10$ feet.

The perimeter of the right triangle is therefore

feet.

The octagon has perimeter 20% greater than this, or

$60 + 0.20 \times 60 = 60 + 12 = 72$ feet.

A regular octagon has eight sides of equal length, so each side of this octagon has length

$72 \div 8 = 9$ feet, which is equal to 3 yards. This makes the quantities equal.

Compare your answer with the correct one above

Question

The area of a square is equal to that of the above right triangle. Which is the greater quantity?

(A) The sidelength of the square

(B) 4 yards

Answer

By the Pythagorean Theorem, the shorter leg has length

$\sqrt{26^{2}-24^{2}} = \sqrt{676-576} = \sqrt{100} = 10$ feet.

The area of a triangle is equal to half the product of its base and height; for a right triangle, the legs can serve as these. The area of the above right triangle is

$\frac{1}{2} \times 10 \times 24 = 120$ square feet.

The sidelength is the square root of this; , so $\sqrt{120} < \sqrt{121} = 11$ . Therefore each sidelength of the square is just under 11 feet. 4 yards is 12 feet, so (B) is greater.

Compare your answer with the correct one above

Question

Consider a triangle, $\bigtriangleup ABC$ , in which , , and $m \angle B = 100 ^{\circ}$ . Which is the greater quantity?

(a) 55

(b)

Answer

Suppose .

By the Converse of the Pythagorean Theorem, a triangle is right if and only if the sum of the squares of the lengths of the smallest two sides is equal to the square of the longest side. Compare the quantities $(AB)^{2}+ ( BC )^{2}$ and $(AC)^{2}$

$(AB)^{2}+ ( BC )^{2} = 33^{2} + 44 ^{2} = 1,089+ 1,936= 3,025$

$(AC)^{2} = 55^{2} = 3,025$

Therefore, if

$(AB)^{2}+ ( BC )^{2} =(AC)^{2}$ , so $\bigtriangleup ABC$ is right, with the right angle opposite longest side $\overline{AC}$ . Thus, $\angle B$ is right and has degree measure 90.

However, $\angle B$ has degree measure greater than 90, so, as a consequence of the Converse of the Pythagorean Theorem and the SAS Inequality Theorem, it holds that .

Compare your answer with the correct one above

Tap the card to reveal the answer