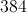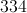How to find the perimeter of a polygon
Help Questions
Math › How to find the perimeter of a polygon
Explanation
The perimeter of the polygon is 46. Think of this polygon as a rectangle with two of its corners "flipped" inwards. This "flipping" changes the area of the rectangle, but not its perimeter; therefore, the top and bottom sides of the original rectangle would be 12 units long 

What is the perimeter of a regular nonagon with a side length of 
Explanation
To find the perimeter of a regular polygon, we take the length of each side, 

In a nonagon the number of sides is 

The perimeter is 
Find the perimeter of the following octagon:

Explanation
The formula for the perimeter of an octagon is 
Plugging in our values, we get:
What is the perimeter of a regular hendecagon with a side length of 32?
Explanation
To find the perimeter of a regular hendecagon you must first know the number of sides in a hendecagon is 11.
When you know the number of sides of a regular polygon to find the perimeter you must multiply the side length by the number of sides.
In this case it is 
The answer for the perimeter is 

 is 10. The length of segment
is 10. The length of segment  is 8. The length of segment
is 8. The length of segment  is 3. The length of segment
is 3. The length of segment  is 2.
is 2.