How to find the length of the side of a right triangle
Help Questions
Math › How to find the length of the side of a right triangle
The legs of a right triangle are 

Explanation
Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Explanation
Given a right triangle with a leg length of 6 and a hypotenuse length of 10, find the length of the other leg, x.

8
16
4
64
Explanation
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 62 = 102
Now we solve for x:
_x_2 + 36 = 100
_x_2 = 100 – 36
_x_2 = 64
x = 8
Also note that this is proportionally a 3/4/5 right triangle, which is very common. Always look out for a side-to-hypoteneuse ratio of 3/5 or 4/5, or a side-to-side ratio of 3/4, in any right triangle, so that you may solve such triangles rapidly.
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
33
42
15
12 √6
33√2
Explanation
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

2
6
√8
10
4
Explanation
Using Pythagorean Theorem, we can solve for the length of leg x:
_x_2 + 22 = (√8)2 = 8
Now we solve for x:
_x_2 + 4 = 8
_x_2 = 8 – 4
_x_2 = 4
x = 2
A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.

3.5
4
4.5
5
5.5
Explanation
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
10
11
12
13
14
Explanation
We can use the Pythagorean Theorem to solve for x.
92 + _x_2 = 152
81 + _x_2 = 225
_x_2 = 144
x = 12
Explanation
The length of segment 
Note that triangles 






which simplifies to 
In a right triangle a hypotenuse has a length of 8 and leg has a length of 7. What is the length of the third side to the nearest tenth?
1.0
3.9
2.4
3.6
Explanation
Using the pythagorean theorem, 82=72+x2. Solving for x yields the square root of 15, which is 3.9




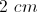










 ,
,  , and
, and  are collinear (they lie along the same line).
are collinear (they lie along the same line).  ,
,  ,
,  ,
, 
 .
.






 .
.






