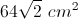The area of a circle is given by A = πr2 or 22/7r2

The area of a square is given by A = s2 or (2r)2 = 4r2

Then subtract the area of the circle from the area of the square and get 6/7 square units.

Since the yard is square in shape, we can divide the perimeter(140ft) by 4, giving us 35ft for each side. We then square 35 to give us the area, 1225 feet.

A few facts need to be known to solve this problem. Observe that the diagonal of the square cuts it into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse: .

Rearrange an solve for .

Now, solve for the area using the formula .

Assign variables such that

One side of ABCD = a

and One side of EFGH = e

Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:

4a = 3 x 4e = 12e or a = 3e

From that area of EFGH is 25,

e x e = 25 so e = 5

Substitute a = 3e so a = 15

We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.

Area of a square in terms of each of its sides:

Area = S x S

Perimeter of a square:

Perimeter = 4S

So if 'the perimeter of a square is equal to twice its area':

2 x Area = Perimeter

2 x \[S x S\] = \[4S\]; divide by 2:

S x S = 2S; divide by S:

S = 2

The formula for the area of a square is . However, the problem gives us a diagonal and not a side.

Remember that all sides of a square are equal, so the diagonal cuts the square into two equal triangles, each a right triangle.

If we use the Pythagorean Theorem, we see:

Plug in our given diagonal to solve.

From here we can plug our answer back into our original equation:

This is an isosceles right triangle, so the diagonal must equal times the length of a side. Thus, one side of the square measures , and the area is equal to

If the area of the half circle is , then the area of a full circle is twice that, or .

Use the formula for the area of a circle to solve for the radius:

36π = πr2

r = 6

If the radius is 6, then the diameter is 12. We know that the sides of the square are the same length as the diameter, so each side has length 12.

Therefore the area of the square is 12 x 12 = 144.

Express the ratio of the two sides of the squares as . The area of each square is one side multiplied by itself, so the ratios of the areas would be . The right side of this equation simplifies to a ratio of .

The area of a square is equal to its length times its width, so we need to figure out how long each side of the parking lot is. Since a square has four sides we calculate each side by dividing its perimeter by four.

Each side of the square lot will use 40 feet of fence.

.