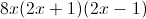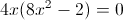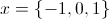Factoring Polynomials
Help Questions
Math › Factoring Polynomials
Factor the following polynomial:
Explanation
Begin by separating 


Now, extract like terms:
Simplify:
Factor the following polynomial:
Explanation
To begin, distribute the squares:
Now, combine like terms:
Factor the following polynomial:
Explanation
Begin by extracting 
Now, distribute the cubic polynomial:
Factor
Cannot be Factored
Explanation
Use the difference of perfect cubes equation:
In 

Factor this expression:
Explanation
First consider all the factors of 12:
1 and 12
2 and 6
3 and 4
Then consider which of these pairs adds up to 7. This pair is 3 and 4.
Therefore the answer is 
Factor the following polynomial:
Explanation
Begin by extracting like terms:
Now, rearrange the right side of the polynomial by reversing the signs:
Combine like terms:
Factor the square and cubic polynomial:
Factor the following polynomial:
Explanation
Begin by rearranging the terms to group together the quadratic:
Now, convert the quadratic into a square:
Finally, distribute the 
Factor the following polynomial:
Explanation
Begin by extracting 
Now, rearrange to combine like terms:
Extract the like terms and factor the cubic:
Simplify by combining like terms:
Factor the following polynomial:
Explanation
Begin by extracting 
Now, rearrange to combine like terms:
Extract the like terms and factor the cubic:
Simplify by combining like terms:
Factor the polynomial completely and solve for 
Explanation
To factor and solve for 
Factor 
Use the "difference of squares" technique to factor the parenthetical term, which provides the completely factored equation:
Any value that causes any one of the three terms 



















![[(3a-4b)+(a+3b)][(3a-4b)-(a+3b)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153192/gif.latex)












![b=\sqrt[3]{64}=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/94643/gif.latex)



































![mn[(m-n)(m^2+mn+n^2)+1(m-n)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153204/gif.latex)







![3[(x+1)(x^2-x+1)+3x(x+1)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153208/gif.latex)
![3[(x+1)(x^2-x+1+3x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/153209/gif.latex)