Vectors - GRE Quantitative Reasoning
Card 0 of 400
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 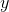 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 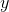 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 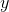 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 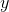 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given, the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 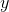 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given, the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 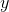 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given, the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 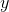 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients. That is, given
coefficients. That is, given , the vector form is
, the vector form is  . So for
. So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients. That is, given
, the vector form is
. So for


Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 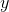 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients. That is, given
coefficients. That is, given , the vector form is
, the vector form is  . So for
. So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients. That is, given
, the vector form is
. So for


Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 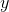 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients. That is, given
coefficients. That is, given , the vector form is
, the vector form is  . So for
. So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients. That is, given
, the vector form is
. So for


Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 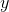 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 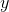 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 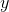 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
Express  in vector form.
in vector form.
Express 
In order to express  in vector form, we must use the coefficients of
in vector form, we must use the coefficients of  and
and  to represent the
to represent the  -,
-,  -, and
-, and  -coordinates of the vector.
-coordinates of the vector.
Therefore, its vector form is
 .
.
In order to express 





Therefore, its vector form is

Compare your answer with the correct one above
Express  in vector form.
in vector form.
Express 
In order to express  in vector form, we must use the coefficients of
in vector form, we must use the coefficients of  and
and  to represent the
to represent the  -,
-,  -, and
-, and  -coordinates of the vector.
-coordinates of the vector.
Therefore, its vector form is
 .
.
In order to express 





Therefore, its vector form is

Compare your answer with the correct one above
Express  in vector form.
in vector form.
Express 
The correct form of x,y, and z of a vector is represented in the order of i, j, and k, respectively. The coefficients of i,j, and k are used to write the vector form.

The correct form of x,y, and z of a vector is represented in the order of i, j, and k, respectively. The coefficients of i,j, and k are used to write the vector form.
Compare your answer with the correct one above
Express  in vector form.
in vector form.
Express 
The x,y, and z of a vector is represented in the order of i, j, and k, respectively. Use the coefficients of i,j, and k to write the vector form.

The x,y, and z of a vector is represented in the order of i, j, and k, respectively. Use the coefficients of i,j, and k to write the vector form.
Compare your answer with the correct one above
Find the vector form of  to
to  .
.
Find the vector form of 

When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given  and
and 
![\overrightarrow{v}=[d-a, e-b, f-c]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327010/gif.latex)
In our case we have ending point at  and our starting point at
and our starting point at  .
.
Therefore we would set up the following and simplify.
![\overrightarrow{v}=[6-0,3-1,1-3]=[6,2,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327013/gif.latex)
When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given 
In our case we have ending point at 

Therefore we would set up the following and simplify.
Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 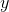 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
What is the vector form of  ?
?
What is the vector form of 
In order to derive the vector form, we must map the  ,
, 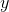 ,
,  -coordinates to their corresponding
-coordinates to their corresponding  ,
,  , and
, and  coefficients.
coefficients.
That is, given  , the vector form is
, the vector form is  .
.
So for  , we can derive the vector form
, we can derive the vector form  .
.
In order to derive the vector form, we must map the ,
,
-coordinates to their corresponding
,
, and
coefficients.
That is, given , the vector form is
.
So for 

Compare your answer with the correct one above
Calculate the dot product of the following vectors:


Calculate the dot product of the following vectors:
Write the formula for dot product given  and
and  .
.

Substitute the values of the vectors to determine the dot product.

Write the formula for dot product given 

Substitute the values of the vectors to determine the dot product.
Compare your answer with the correct one above