Real and Ideal Gases
Help Questions
Physical Chemistry › Real and Ideal Gases
Given the van der Waals Equation:
Which statement accurately identifies and explains the corrections that van der Waals made to the ideal gas law, where the first correction is the 

The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume decreases and number of molecules increases.
The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by decreasing pressure as volume increases and number of molecules increases.
The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume increases and number of molecules increases.
The first correction corrects for volume of molecules by decreasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume increases and number of molecules increases.
The first correction corrects for volume of molecules by increasing volume as a function of the number of molecules, and the second correction corrects for molecular attraction by increasing pressure as volume decreases and number of molecules increases.
Explanation
All the statements say similar things, but only one correctly identifies the resulting change to volume and pressure. Let's break things down by the correction.
Correction 1:
The correction decreases the volume, since it is subtracting 
Correction 2:
Since we are subtracting 



Given the ideal gas law:
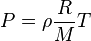
Where 




Based on the Ideal gas law, which of the following are true?
I. Pressure and volume are inversely proportional
II. Pressure and density are inversely proportional
III. Pressure and temperature are directly proportional
IV. Density and temperature are inversely proportional
V. R and M are inversely proportional
I, III, IV
I, II, III, IV, V
I, III
II, III, V
III, IV, V
Explanation
Condition I is true. Pressure and volume are inversely proportional. The ideal gas law with volume can be rederived to show this:
We introduce an expression for moles:
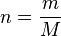
Where 


Rearranging (1) to solve for 
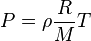
We get:

Finally, we use the following for density, where 
The masses cancel out and we have the ideal gas law expressed with volume and moles.
Condition II is false. It is clear from the equation that pressure and density are directly proportional.
Condition III is true because it is clear from the equation that temperature and pressure are directly proportional.
Condition IV is true because density and temperature are on the same side of the equation in the numerator, so the must be inversely proportional.
Condition V is false because the ideal gas constant and molar mass can be rearranged to be on opposite sides of the equation and in the numerator.
Under which conditions do gases deviate from ideality?
I. Low temperature
II. High temperature
III. Low pressure
IV. High pressure
V. Gases always behave ideally
I and IV
V only
I and III
II and III
II and IV
Explanation
Gases deviate from ideal conditions at low temperature and high pressure. This because the postulates of the kinetic molecular theory of gasses ignore the volume of the molecules and all interactions between gas molecules. However, neither are true for real gasses. As the temperature increases, the kinetic energy of the particles can overcome the intermolecular forces of attraction or repulsion between the molecules. At high pressures, and subsequently low volume, the distance between molecules becomes shorter, and therefore intermolecular forces become significant. So, ideal conditions are when the distance between molecules is great, and the energy each molecule has is much greater in relative magnitude to the intermolecular forces. This occurs when the pressure is low, and the temperature is high.




