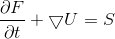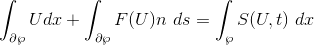Derivatives from Conservation Laws
Help Questions
Differential Equations › Derivatives from Conservation Laws
What is the order of the following partial differential equation.
Second Order
First Order
Third Order
Linear
Quasi Linear
Explanation
Just like with ordinary differential equations, partial differential equations can be characterized by their order.
The order of an equation is defined by the highest ordered partial derivatives in the equations.
Looking at the equation in question,
The partial derivatives are:
Notice that each partial derivative contains two variables, thus this equation is a second order partial differential equation.
What is the conservation law written as a partial differential equation?
Explanation
The conservation law written as a partial differential equation is found by applying the divergence theorem to the conservation equation.
The conservation equation is,
Now, recall the divergence theorem which states,
Thus, by substituting


From here, rewriting this equation to bring the derivative inside the integral along with substituting

and performing some algebraic operations results in,
After integrating over the domain 
What is the order of the following partial differential equation.
Third Order
Second Order
First Order
Homogeneous
Non-homogenous
Explanation
Just like with ordinary differential equations, partial differential equations can be characterized by their order.
The order of an equation is defined by the highest ordered partial derivatives in the equations.
Looking at the equation in question,
The partial derivatives are:
Notice that one of them partial derivative contains three variables, thus this equation is a third order partial differential equation.
Which of the following describes the physical phenomena that is the biharmonic wave equation?
Explanation
When dealing with partial differential equations, there are phenomenons in the physical world that have specific equations related to them in the mathematical world.
Looking at the possible answer selections below, identify the physical phenomena each represents.





Therefore, the correct answer for the biharmonic wave equation is
What is the order of the following partial differential equation.
Third Order
Second Order
First Order
Linear
Quasi Linear
Explanation
Just like with ordinary differential equations, partial differential equations can be characterized by their order.
The order of an equation is defined by the highest ordered partial derivatives in the equations.
Looking at the equation in question,
The partial derivatives are:
Notice that one of them partial derivative contains three variables, thus this equation is a third order partial differential equation.