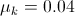MCAT Physical - Newtonian Mechanics and Motion

A force of is applied to a block with a mass of on a frictionless surface. What is the acceleration of the block?

$4\frac{m}{s^{2}}$

$5\frac{m}{s^{2}}$

$100\frac{m}{s^{2}}$

The block moves with a constant velocity

Explanation

For this question we must use Newton's second law. We have to use the formula .

is the force being applied, is the mass of the object, and is the acceleration of the object

$20N = 5kg \cdot a$

$a = \frac{20N}{5kg}$

$a = 4 \frac{m}{s^{2}}$

A 2kg box is at the top of a ramp at an angle of 60o. The top of the ramp is 30m above the ground. The box is sitting still while at the top of the ramp, and is then released.

Imagine that the net force on the box is 16.5N when sliding down the ramp. What is the coefficient of kinetic friction for the box?

$\mu_k=0.08$

$\mu_k=0.16$

The kinetic coefficient of friction cannot be determined while the box is moving

$\mu_k=0.04$

Explanation

Since the box is moving when the net force on the box is determined, we can calculate the coefficient of kinetic friction for the box. The first step is determining what the net force on the box would be in the absence of friction. The net force on the box is given by the equation $\small F = mgsin\Theta$ .

$\small F = (2kg)(10\frac{m}{s^{2}})sin(60^{\circ}) = 17.3N.$

The difference between the frictionless net force and the net force with friction is 0.8N. This means that the force of kinetic friction on the box is 0.8N, acting opposite the direction of motion. Knowing this, we can solve for the coefficient of kinetic friction using the equation $\small f_{k} = \mu_{k}F_{n}$

$\small 0.8 = (mgcos\Theta)(\mu _{k})$

$\small 0.8 = (2kg)(10cos(60^{\circ}))\mu_{k}$

$\small \mu_{k} = 0.08$

When the force applied to a moving object is equal and opposite the force of kinetic friction, what happens to the object?

It moves with a constant velocity

It stops

It accelerates

It decelerates

It changes direction

Explanation

It is important to understand the difference between static and kinetic friction. When an object is at rest, it takes more force to get it to start moving than to keep it moving. If you match the amount of static friction that can be generated when the object is at rest, it will not move because there is zero net force; the force applied must be greater than the static friction in order to initiate motion. Once the object begins moving, the force required to keep it moving decreases. If you match the force of kinetic friction, the object moves at a constant velocity because there is again no net force. Any more force will cause acceleration, while any less will cause deceleration.

A 3kg book slides towards the right along a frictionless horizontal surface with initial velocity 5m/s, then suddenly encounters a long rough section with kinetic friction coefficient $\mu=0.25$ . How far does the book travel along the rough surface before coming to rest? (Use $\small \small g = 9.8\frac{m}{s^{2}}$ as needed)

5.1m

4.4m

3.7m

2.9m

6.5m

Explanation

We'll need to use the kinematic equation $\small v_{f}^{2}=v_{i}^{2}+2ad$ to solve for d, the distance travelled when the book has stopped ( $\small v_{f}=0$ ). Before solving for d, we need to calculate the acceleration caused by the frictional force, by using the following steps.

Find the normal force on the book, $\small F_{n}=mg$ .
Plug this normal force into $\small F_{f}=\mu_{k}F_{n}$ to solve for frictional force.
Find the acceleration caused by this frictional force, with $\small F_{f}=ma$ .

Step 1 gives $\small \small F_{n}=29.4N$ , so in step 2, $\small \small F_{f}=7.35N$ , giving an acceleration of $\small a = 2.45\frac{m}{s^{2}}$ to the left (which we will define to be the negative horizontal direction).

Returning to the original kinematic equation, $\small 0 =(5 \frac{m}{s})^{2} + 2(-2.45\frac{m}{s^{2}})d$ .

Rearranging to solve for d gives $\small d = 5.1m$

A 50kg block resting on the ground experiences an upward acceleration of 4m/s2. What is the normal force acting on the block?

300 N

200 N

700 N

500 N

Explanation

The block experiences the force of gravity, plus the force of the upward acceleration

$Fnet = (50kg)(-10m/s^{2}) + (50kg)(4m/s^{2}) = -300 N$

If the block is resting on the ground, then its total force must be zero, and the normal force must cancel out the net force above. The normal force is 300N.

Suppose a ball with mass of 10kg was dropped from rest from the top of a cliff that is 80m tall. How long will it take the ball to reach the bottom of the cliff?

10s

16s

Explanation

The question tells us that the initial velocity of the ball (v0) is zero and the height (d) of the cliff is 80m. Acceleration (gravity) is 10m/s2. Using the kinematics eqation $d=v_0 t+(1/2)at^{2}$ we can solve for time.

80 = 0 + (1/2)(10)t2

80/5 = t2 = 16

t = 4s

5.1m

4.4m

3.7m

2.9m

6.5m

Explanation

Find the normal force on the book, $\small F_{n}=mg$ .
Plug this normal force into $\small F_{f}=\mu_{k}F_{n}$ to solve for frictional force.
Find the acceleration caused by this frictional force, with $\small F_{f}=ma$ .

Returning to the original kinematic equation, $\small 0 =(5 \frac{m}{s})^{2} + 2(-2.45\frac{m}{s^{2}})d$ .

Rearranging to solve for d gives $\small d = 5.1m$

Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.

Over the course of the afternoon, they collide many times. Four collisions are described below.

Collision 1:

Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 5m/s and subsequently slides into a stationary child 2. They remain linked together after the collision.

Collision 2:

Child 1 and child 2 are sliding in the same direction. Child 2, moving at 10m/s, slides into child 1, moving at 2m/s.

Collision 3:

The two children collide while traveling in opposite directions at 10m/s each.

Collision 4:

The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of +8m/s.

Child 1 hooks up a jet motor to a sled, and brings it to the icy lake. She sets up her sled, and launches from a velocity of 8m/s with an acceleration of 15m/s2. After fifteen seconds, how far has she traveled?

1.8km

1800km

1.8m

600km

600m

Explanation

For this question, we have to use a translational motion equation.

A ball with mass of 2kg is dropped from the top of a building this is 30m high. What is the approximate velocity of the ball when it is 10m above the ground?

20m/s

25m/s

14m/s

10m/s

30m/s

Explanation

Use conservation of energy. The gravitational potential energy lost as the ball drops from 30m to 10m equals the kinetic energy gained.

Change in gravitational potential energy can be found using the difference in mgh. $mgh_{f} - mgh_{i} = 2kg*10\frac{m}{s^{2}}*10m - 2kg*10\frac{m}{s^{2}}*30m = -400 Joules$

So 400 Joules are converted from gravitational potential to kinetic energy, allowing us to solve for the velocity, v.

$400 Joules = \frac{1}{2}mv^{2}$

$400 = v^{2}$

$v = 20 m/s$

An empty mining cart has a mass of and is traveling down a track that has a slope of $40^{\circ}$ to the horizontal. The cart is traveling at a rate of $10\frac{m}{s}$ when an operator notices a disturbance on the track ahead and locks the wheels of the cart. What is the speed of the cart after it has traveled with the wheels locked?

$\mu_s = 0.6,\ \mu_k=0.3$

$g=10\frac{m}{s^2}$

$16.3\frac{m}{s}$

$13.2\frac{m}{s}$

$6.8\frac{m}{s}$

$4.7\frac{m}{s}$

$8.3\frac{m}{s}$

Explanation

We need the equation for conservation of energy for this problem:

We can eliminate final potential energy if we set the final height to be zer. We are solving for final velocity, so let's rearrange for final kinetic energy.

Substituting our equations for each variable, we get:

$\frac{1}{2}mv_f^2 = mgh_i + \frac{1}{2}mv_i^2 - \mu_kNd$

Rearranging for final velocity we get:

$v_f = \sqrt{2gh_i+v_i^2-\frac{2\mu_kNd}{m}}$

If you derive this formula and are unsure of your work, simply check your units. Each term under the square root has units of $\frac{m^2}{s^2}$ , which will ultimately give us units of $\frac{m}{s}$ , which is what we want.

We have values for all variables except two: height and normal force.

Let's calculate the height. We know that the between the initial and final states, the cart has traveled 20 meters down a slope of 40 degrees. Therefore, we can calculate height with the formula:

$sin(40^{\circ})=\frac{h_i}{20 m}$

Now we just need to find the normal force. The following diagram will help visualize this calculation.

If you are unsure whether to use sine or cosine, think about it practically. As the angle gets less and less, the normal force is going to get larger. This is characteristic of a cosine function.

Therefore, we can say that:

$N = mgcos(40^{\circ}) = (15kg)(10\frac{m}{s^2})cos(40^{\circ})= 114.9 N$

Now that we have all of our variables, it's time to plug and chug:

$v_f=\sqrt{(2\cdot10\cdot12.856)+(10)^2-\frac{2\cdot0.3\cdot114.9\cdot20}{15}}$

$v_f=\sqrt{257.1+100-91.9} = 16.3 \frac{m}{s}$

Newtonian Mechanics and Motion

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation