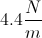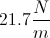Work, Energy, and Power

Help Questions

MCAT Physical › Work, Energy, and Power

Questions 1 - 10

An empty mining cart has a mass of and is traveling down a track that has a slope of $40^{\circ}$ to the horizontal. The cart is traveling at a rate of $10\frac{m}{s}$ when an operator notices a disturbance on the track ahead and locks the wheels of the cart. What is the speed of the cart after it has traveled with the wheels locked?

$\mu_s = 0.6,\ \mu_k=0.3$

$g=10\frac{m}{s^2}$

$16.3\frac{m}{s}$

$13.2\frac{m}{s}$

$6.8\frac{m}{s}$

$4.7\frac{m}{s}$

$8.3\frac{m}{s}$

Explanation

We need the equation for conservation of energy for this problem:

We can eliminate final potential energy if we set the final height to be zer. We are solving for final velocity, so let's rearrange for final kinetic energy.

Substituting our equations for each variable, we get:

$\frac{1}{2}mv_f^2 = mgh_i + \frac{1}{2}mv_i^2 - \mu_kNd$

Rearranging for final velocity we get:

$v_f = \sqrt{2gh_i+v_i^2-\frac{2\mu_kNd}{m}}$

If you derive this formula and are unsure of your work, simply check your units. Each term under the square root has units of $\frac{m^2}{s^2}$ , which will ultimately give us units of $\frac{m}{s}$ , which is what we want.

We have values for all variables except two: height and normal force.

Let's calculate the height. We know that the between the initial and final states, the cart has traveled 20 meters down a slope of 40 degrees. Therefore, we can calculate height with the formula:

$sin(40^{\circ})=\frac{h_i}{20 m}$

Now we just need to find the normal force. The following diagram will help visualize this calculation.

If you are unsure whether to use sine or cosine, think about it practically. As the angle gets less and less, the normal force is going to get larger. This is characteristic of a cosine function.

Therefore, we can say that:

$N = mgcos(40^{\circ}) = (15kg)(10\frac{m}{s^2})cos(40^{\circ})= 114.9 N$

Now that we have all of our variables, it's time to plug and chug:

$v_f=\sqrt{(2\cdot10\cdot12.856)+(10)^2-\frac{2\cdot0.3\cdot114.9\cdot20}{15}}$

$v_f=\sqrt{257.1+100-91.9} = 16.3 \frac{m}{s}$

A 2kg lead ball is loaded into a spring cannon and the cannon is set at a 45º angle on a platform. The spring has a spring constant of 100N/m and the ball and spring system is compressed by 1m before launch. While the ball is in flight air resistance can be neglected, and the ball finishes its flight by landing at a cushion placed some distance away from the cannon.

How much energy is stored in the spring before the ball is launched?

50J

50kJ

20J

20kJ

Explanation

In order to determine how much energy is stored, we first need to understand what type of energy we want to consider. A spring stores potential energy; the potential energy of the spring is maximized at maximal displacement from its resting state. In order to compute the potential energy stored, we need both the spring constant (100N/m) and the displacement from resting (1m).

PEs = ½k(Δx)2 = ½(100N/m)(1m)2 = 50J

A ball with mass of 2kg is dropped from the top of a building this is 30m high. What is the approximate velocity of the ball when it is 10m above the ground?

20m/s

25m/s

14m/s

10m/s

30m/s

Explanation

Use conservation of energy. The gravitational potential energy lost as the ball drops from 30m to 10m equals the kinetic energy gained.

Change in gravitational potential energy can be found using the difference in mgh. $mgh_{f} - mgh_{i} = 2kg*10\frac{m}{s^{2}}*10m - 2kg*10\frac{m}{s^{2}}*30m = -400 Joules$

So 400 Joules are converted from gravitational potential to kinetic energy, allowing us to solve for the velocity, v.

$400 Joules = \frac{1}{2}mv^{2}$

$400 = v^{2}$

$v = 20 m/s$

What is the work done by gravity if a 50kg block is pushed along a 40m track?

Explanation

The work done by any force that is perpendicular to the displacement is equal to zero. Since the block is moving horizontally, the net force in the vertical direction will be equal to zero; therefore, work done by either gravity or the normal force will be equal to zero.

$W_g=(10\frac{m}{s^2})(0m)=0J$

Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.

Over the course of the afternoon, they collide many times. Four collisions are described below.

Collision 1:

Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going $5\frac{m}{s}$ and subsequently slides into a stationary child 2. They remain linked together after the collision.

Collision 2:

Child 1 and child 2 are sliding in the same direction. Child 2, moving at $10\frac{m}{s}$ , slides into child 1, moving at $2\frac{m}{s}$ .

Collision 3:

The two children collide while traveling in opposite directions at $10\frac{m}{s}$ each.

Collision 4:

The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of $+8\frac{m}{s}$ .

Before collision 3 takes place, suppose that child 1 starts at the top of a ramp that is 3m long, and to the lake surface.

With what speed does child 1 hit the lake surface? Ignore friction and air resistance.

$5.4\frac{m}{s}$

$0.9\frac{m}{s}$

$55\frac{m}{s}$

$900\frac{m}{s}$

$9.8\frac{m}{s}$

Explanation

This is an application of the work-energy theorem. The amount of work done by the force of gravity to move child 1 down the ramp is equal to force * distance, as well as equal to the amount of kinetic energy picked up down the ramp.

The force down the ramp is equal to mg*sin(30o) = 600J * 0.5 = 300J

A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of . The coefficient of kinetic friction for the ramp is 0.1.

What is the work done on the box by friction?

Explanation

Because the force of friction is parallel to the displacement of the box, we can solve for the work done by friction using the following equation.

$W=F\cdot d$

Now, we need to define the force of friction or $F_{f}$ .

$F_f=\mu\cdot m \cdot a$

In this formula, equals acceleration. In this case, acceleration equals acceleration due to gravity in the x-direction; therefore, use the cosine function.

$F_{f}=(0.1)\cdot(2kg)\cdot (g\cdot \cos(30^o))$

Insert the value of acceleration due to gravity for .

$F_{f}=0.1\cdot 2kg \cdot -9.8\tfrac{m}{s^2}\cdot \cos(30^o)$

Now, we can solve for the work done by friction.

$W_{friction} =F_f\cdot d$

$W_{friction}=(-1.697N)\cdot(2m)$

$W_{friction} = -3.39J$

A ball with mass of 2kg is dropped from the top of a building this is 30m high. What is the approximate velocity of the ball when it is 10m above the ground?

20m/s

25m/s

14m/s

10m/s

30m/s

Explanation

Use conservation of energy. The gravitational potential energy lost as the ball drops from 30m to 10m equals the kinetic energy gained.

Change in gravitational potential energy can be found using the difference in mgh. $mgh_{f} - mgh_{i} = 2kg*10\frac{m}{s^{2}}*10m - 2kg*10\frac{m}{s^{2}}*30m = -400 Joules$

So 400 Joules are converted from gravitational potential to kinetic energy, allowing us to solve for the velocity, v.

$400 Joules = \frac{1}{2}mv^{2}$

$400 = v^{2}$

$v = 20 m/s$

A massless spring rests horizontally on a table, with its right end attached to a $\small 250g$ block and with its left end attached to a wall. The block is then pushed against the spring, compressing it $\small 15cm$ from its equilibrium position. After being released, the block's velocity as it moves back through the equilibrium point is $\small 2\frac{m}{s}$ . What is the spring constant of this spring?

$44.4\frac{N}{m}$

$3.2\frac{N}{m}$

$4.4\frac{N}{m}$

$21.7\frac{N}{m}$

$89.3\frac{N}{m}$

Explanation

Use conservation of energy to equate the initial spring potential energy and the final kinetic energy:

$K_{i} +U_{i}=K_{f}+U_{f}$

The initial situation is defined when the spring and block are compressed, and the final situation is defined to be when the block moves back through the equilibrium point. For a spring, the potential energy is maximal when the spring is compressed and the kinetic energy is maximal when the mass passes equilibrium. We can set up a equation based on these factors.

$K_i=0\ \text{and}\ U_f=0$

Use the equations for spring potential energy and for kinetic energy to incorporate the appropriate variables into the equation.

$U=\frac{1}{2}kx^2\ \text{and}\ KE=\frac{1}{2}mv^2$

$\frac{1}{2}kx_i^2=\frac{1}{2}mv_f^2$

We are given values for the displacement, mass, and final velocity. Using these values, we can isolate the spring constant.

$\frac{1}{2}k(0.15m)^2=\frac{1}{2}(0.25kg)(2\frac{m}{s})^2$

$k=44.4\frac{N}{m}$

$44.4\frac{N}{m}$

$3.2\frac{N}{m}$

$4.4\frac{N}{m}$

$21.7\frac{N}{m}$

$89.3\frac{N}{m}$

Explanation

Use conservation of energy to equate the initial spring potential energy and the final kinetic energy:

$K_{i} +U_{i}=K_{f}+U_{f}$

$K_i=0\ \text{and}\ U_f=0$

Use the equations for spring potential energy and for kinetic energy to incorporate the appropriate variables into the equation.

$U=\frac{1}{2}kx^2\ \text{and}\ KE=\frac{1}{2}mv^2$

$\frac{1}{2}kx_i^2=\frac{1}{2}mv_f^2$

We are given values for the displacement, mass, and final velocity. Using these values, we can isolate the spring constant.

$\frac{1}{2}k(0.15m)^2=\frac{1}{2}(0.25kg)(2\frac{m}{s})^2$

$k=44.4\frac{N}{m}$

Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.

Over the course of the afternoon, they collide many times. Four collisions are described below.

Collision 1:

Collision 2:

Child 1 and child 2 are sliding in the same direction. Child 2, moving at $10\frac{m}{s}$ , slides into child 1, moving at $2\frac{m}{s}$ .

Collision 3:

The two children collide while traveling in opposite directions at $10\frac{m}{s}$ each.

Collision 4:

The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of $+8\frac{m}{s}$ .

Before collision 3 takes place, suppose that child 1 starts at the top of a ramp that is 3m long, and to the lake surface.

With what speed does child 1 hit the lake surface? Ignore friction and air resistance.

$5.4\frac{m}{s}$

$0.9\frac{m}{s}$

$55\frac{m}{s}$

$900\frac{m}{s}$

$9.8\frac{m}{s}$