Translational Motion
Help Questions
MCAT Physical › Translational Motion
Two astronauts, Ann and Bob, conduct a collision experiment in a weightless, frictionless environment. Initially Ann moves to the right with a momentum of 


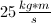



Explanation
Apply conservation of momentum before and after the collision.

Taking left to be the negative direction, and noting that Bob's initial momentum is 0 since he is at rest, we can use the provided information to see that 
Solving for 

Suppose a ball with mass of 10kg was dropped from rest from the top of a cliff that is 80m tall. How long will it take the ball to reach the bottom of the cliff?
4s
10s
2s
8s
16s
Explanation
The question tells us that the initial velocity of the ball (v0) is zero and the height (d) of the cliff is 80m. Acceleration (gravity) is 10m/s2. Using the kinematics eqation 
80 = 0 + (1/2)(10)t2
80/5 = t2 = 16
t = 4s
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 5m/s and subsequently slides into a stationary child 2. They remain linked together after the collision.
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 10m/s, slides into child 1, moving at 2m/s.
Collision 3:
The two children collide while traveling in opposite directions at 10m/s each.
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of +8m/s.
Child 1 hooks up a jet motor to a sled, and brings it to the icy lake. She sets up her sled, and launches from a velocity of 8m/s with an acceleration of 15m/s2. After fifteen seconds, how far has she traveled?
1.8km
1800km
1.8m
600km
600m
Explanation
For this question, we have to use a translational motion equation.
Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.
They then decide to sled down the hill, but disagree about who will go first.
Scenario 1:
Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.
Scenario 2:
Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.
Scenario 3:
Unable to agree, Sam and Sally tether themselves with a rope and go down together.
If the hill is frictionless, what momentum does Sam experience when he reaches the bottom of the 50m hill on his sled in Scenario 1?
1898kg*m/s
60kg*m/s
1581kg*m/s
1340kg*m/s
0kg*m/s
Explanation
The momentum is equal to Sam's total mass times his velocity. His velocity can be found from his potential energy, using conservation of energy. Keep in mind, his total mass includes the mass of his sled.
PE = mgh = (50kg + 10kg) * 10m/s2 * 50m
PE = 30,000J
KE = 30,000J = 1/2mv2 = 1/2(60kg)(v2)
v2 = 1000 m2/s2 = 31.2m/s
p = mv = 60 kg * 31.2 m/s = 1898 kg*m/s
If you had used 30J in place of 30kJ in the KE calculation, you would have chosen 60kg*m/s
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 

Collision 3:
The two children collide while traveling in opposite directions at 
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of 
In all of the above scenarios, which of the following quantities is conserved?
I. Kinetic energy
II. Potential energy
III. Momentum
III only
I and II
II and III
I and III
I, II, and III
Explanation
Kinetic energy and potential energy are interconverted. While total energy is conserved, kinetic energy is allowed to increase or decrease, provided that potential energy does the opposite. For example, as the child in collision 1 is starting at the top of a ramp, she has potential energy, but no kinetic energy. At the bottom of the ramp, all the potential energy has been turned into kinetic energy.
Momentum, on the other hand, is conserved in every collision.
Two astronauts, Ann and Bob, conduct a collision experiment in a weightless, frictionless environment. Initially Ann moves to the right with a momentum of 


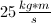



Explanation
Apply conservation of momentum before and after the collision.

Taking left to be the negative direction, and noting that Bob's initial momentum is 0 since he is at rest, we can use the provided information to see that 
Solving for 

Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 5m/s and subsequently slides into a stationary child 2. They remain linked together after the collision.
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 10m/s, slides into child 1, moving at 2m/s.
Collision 3:
The two children collide while traveling in opposite directions at 10m/s each.
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of +8m/s.
Child 1 hooks up a jet motor to a sled, and brings it to the icy lake. She sets up her sled, and launches from a velocity of 8m/s with an acceleration of 15m/s2. After fifteen seconds, how far has she traveled?
1.8km
1800km
1.8m
600km
600m
Explanation
For this question, we have to use a translational motion equation.
Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.
They then decide to sled down the hill, but disagree about who will go first.
Scenario 1:
Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.
Scenario 2:
Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.
Scenario 3:
Unable to agree, Sam and Sally tether themselves with a rope and go down together.
If the hill is frictionless, what momentum does Sam experience when he reaches the bottom of the 50m hill on his sled in Scenario 1?
1898kg*m/s
60kg*m/s
1581kg*m/s
1340kg*m/s
0kg*m/s
Explanation
The momentum is equal to Sam's total mass times his velocity. His velocity can be found from his potential energy, using conservation of energy. Keep in mind, his total mass includes the mass of his sled.
PE = mgh = (50kg + 10kg) * 10m/s2 * 50m
PE = 30,000J
KE = 30,000J = 1/2mv2 = 1/2(60kg)(v2)
v2 = 1000 m2/s2 = 31.2m/s
p = mv = 60 kg * 31.2 m/s = 1898 kg*m/s
If you had used 30J in place of 30kJ in the KE calculation, you would have chosen 60kg*m/s
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 

Collision 3:
The two children collide while traveling in opposite directions at 
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of 
In all of the above scenarios, which of the following quantities is conserved?
I. Kinetic energy
II. Potential energy
III. Momentum
III only
I and II
II and III
I and III
I, II, and III
Explanation
Kinetic energy and potential energy are interconverted. While total energy is conserved, kinetic energy is allowed to increase or decrease, provided that potential energy does the opposite. For example, as the child in collision 1 is starting at the top of a ramp, she has potential energy, but no kinetic energy. At the bottom of the ramp, all the potential energy has been turned into kinetic energy.
Momentum, on the other hand, is conserved in every collision.
Suppose a ball with mass of 10kg was dropped from rest from the top of a cliff that is 80m tall. How long will it take the ball to reach the bottom of the cliff?
4s
10s
2s
8s
16s
Explanation
The question tells us that the initial velocity of the ball (v0) is zero and the height (d) of the cliff is 80m. Acceleration (gravity) is 10m/s2. Using the kinematics eqation 
80 = 0 + (1/2)(10)t2
80/5 = t2 = 16
t = 4s

