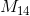Linear Algebra

Help Questions

Linear Algebra › Linear Algebra

Questions 1 - 10

Find the inverse using row operations

$\begin{bmatrix} 2 &7 &1 \-1 &5 &3 \ 2& 2& -1\end{bmatrix}$

$\begin{bmatrix} -11 &9 &16 \5 &-4 & -7\ -12& 10& 17\end{bmatrix}$

$\begin{bmatrix} -15 &9 &16 \7 &-4 & -7\ -16& 10& 17\end{bmatrix}$

$\begin{bmatrix} -11 &9 &16 \5 &-4 & -7\ -16& 10& 17\end{bmatrix}$

$\begin{bmatrix} 1 &0&1 \1&-4 & 1\ -16& 10& 1\end{bmatrix}$

Explanation

To find the inverse, use row operations:

$\begin{bmatrix} 2 &7 &1 &1 &0 &0 \-1 &5 &3 &0 &1 &0 \ 2& 2& -1& 0& 0& 1\end{bmatrix} \sim$ add the third row to the second

$\begin{bmatrix} 2 &7 &1 &1 &0 &0 \1 &7 &2 &0 &1 &1 \ 2& 2& -1& 0& 0& 1\end{bmatrix} \sim$ subtract the second row from the top

$\begin{bmatrix} 1 &0 &-1 &1 &-1 &-1 \1 &7 &2 &0 &1 &1 \ 2& 2& -1& 0& 0& 1\end{bmatrix} \sim$ subtract the first row from the second

$\begin{bmatrix} 1 &0 &-1 &1 &-1 &-1 \0&7 &3 &-1&2 &2 \ 2& 2& -1& 0& 0& 1\end{bmatrix} \sim$ subtract two times the first row from the bottom row

$\begin{bmatrix} 1 &0 &-1 &1 &-1 &-1 \0&7 &3 &-1&2 &2 \ 0& 2& 1& -2& 2&3\end{bmatrix} \sim$ subtract three times the bottom row from the second row

$\begin{bmatrix} 1 &0 &-1 &1 &-1 &-1 \0&1 &0 &5&-4 &-7 \ 0& 2& 1& -2& 2&3\end{bmatrix} \sim$ subtract 2 times the middle row from the bottom row

$\begin{bmatrix} 1 &0 &-1 &1 &-1 &-1 \0&1 &0 &5&-4 &-7 \ 0& 0& 1& -12& 10&17\end{bmatrix} \sim$ add the bottom row to the top

$\begin{bmatrix} 1 &0 &0 &-11 &9&16 \0&1 &0 &5&-4 &-7 \ 0& 0& 1& -12& 10&17\end{bmatrix}$

The inverse is $\begin{bmatrix} -11 & 9& 16\ 5& -4& -7\ -12& 10& 17\end{bmatrix}$

Compute $A\cdot B$ , where

$A=\begin{bmatrix}8&4 \ 2&4 \ 6&1 \end{bmatrix}$ $b=\begin{bmatrix}4&2 \ 4&9 \ 2&1 \end{bmatrix}$

Not Possible

$\begin{bmatrix} 32&16 &8 \ 8&36 &24 \end{bmatrix}$

$\begin{bmatrix} 32&8 \ 8&36 \ 12&1 \end{bmatrix}$

$\begin{bmatrix}8&32 \ 36&8 \ 1&12 \end{bmatrix}$

$\begin{bmatrix} 16\-28 \ 11 \end{bmatrix}$

Explanation

In order to be able to multiply matrices, the number of columns of the 1st matrix must equal the number of rows in the second matrix. Here, the first matrix has dimensions of (3x2). This means it has three rows and two columns. The second matrix has dimensions of (3x2), also three rows and two columns. Since $\tiny \tiny \small 2 eq3$ , we cannot multiply these two matrices together

Calculate the trace.

$\begin{bmatrix} 1&4 \ 5&-1 \end{bmatrix}$

Explanation

The trace of a matrix is simply adding the entries along the main diagonal.

Find the rank of the following matrix.

$\begin{bmatrix} 10 & 2 \ 4 & 5\ 5& 10 \end{bmatrix}$

Explanation

We need to get the matrix into reduced echelon form, and then count all the non all zero rows.

$R_2-\frac{2}{5}R_1\rightarrow R_2$

$\begin{bmatrix} 10 & 2 \ 0 & \frac{21}{5}\ 5& 10 \end{bmatrix}$

$R_3-\frac{1}{2}R_1\rightarrow R_3$

$\begin{bmatrix} 10 & 2 \ 0 & \frac{21}{5}\ 0& 9 \end{bmatrix}$

$R_2 \leftrightarrow R_3$

$\begin{bmatrix} 10 & 2 \ 0& 9 \ 0 & \frac{21}{5}\end{bmatrix}$

$R_3-\frac{7}{15}R_2\rightarrow R_3$

$\begin{bmatrix} 10 & 2 \ 0& 9 \ 0 & 0\end{bmatrix}$

$\frac{1}{9}R_2\rightarrow R_2$

$\begin{bmatrix} 10 & 2 \ 0& 1 \ 0 & 0\end{bmatrix}$

$R_1-2R_2\rightarrow R_1$

$\begin{bmatrix} 10 & 0 \ 0& 1 \ 0 & 0\end{bmatrix}$

$\frac{1}{10}R_1\rightarrow R_1$

$\begin{bmatrix} 1 & 0 \ 0& 1 \ 0 & 0\end{bmatrix}$

The rank is 2, since there are 2 non all zero rows.

$\begin{align*}&\text{Find any and all eigenvalues for the matrix }\&A=\begin{bmatrix}6&-13\8&-19\end{bmatrix}\end{align*}$

$\lambda_{1}=0.73;\lambda_{2}=-13.73$

$\lambda_{1}=1.73;\lambda_{2}=-12.73$

$\lambda_{1}=-3.27;\lambda_{2}=-17.73$

$\lambda_{1}=9.73;\lambda_{2}=-4.73$

Explanation

$\begin{align*}&\text{Eigenvalues of a matrix, typically noted as }\lambda\text{, are those values which satisfy}\&det(A-\lambda I)\text{(I being the identity matrix). For the matrix }A=\begin{bmatrix}6&-13\8&-19\end{bmatrix}\&\text{We can represent that equation as follows }\begin{bmatrix}6 - \lambda &-13\8&- \lambda - 19\end{bmatrix} \&\text{For a square matrix with dimensions of }2\&det\begin{vmatrix} a&b \ c&d \end{vmatrix}=ad-bc\&\text{From that, we can find the eigenvalues:}\&13\lambda + \lambda ^{2} - 10\&\lambda_{1}=0.73;\lambda_{2}=-13.73\end{align*}$

Let be a five-by-five matrix.

Cofactor $C_{14}$ must be equal to:

The additive inverse of Minor $M_{14}$

Minor $M_{14}$

The additive inverse of the reciprocal of Minor $M_{14}$

The reciprocal of Minor $M_{14}$

None of the other choices gives a correct response.

Explanation

The minor of a matrix $M_{mn}$ is the determinant of the matrix formed by striking out Row and Column . By definition, the corresponding cofactor $C_{mn}$ can be calculated from this minor using the formula

$C_{mn}= ( -1 )^{m+n} M_{mn}$

Set ; the formula becomes

$C_{14}= ( -1 )^{1+4} M_{14}$

$C_{14}= ( -1 )^{5} M_{14}$

$C_{14}=-1 \cdot M_{14}$

$C_{14}=- M_{14}$ .

Therefore, the cofactor $C_{14}$ must be equal to the opposite of the minor $M_{14}$ .

$A= \begin{bmatrix} 2 & 3 & 6 \ 0 & 4 & 4 \ 2 & 0 & 4 \end{bmatrix}$ .

Is an eigenvalue of , and if so, what is the dimension of its eigenspace?

No.

Yes; the dimension is 1.

Yes; the dimension is 2.

Yes; the dimension is 3.

Explanation

Assume that is an eigenvalue of . Then, if $b = \begin{bmatrix} b_{1} \ b_{2} \b_{3} \end{bmatrix}$ is one of its eigenvectors, it follows that

, or, equivalently,

where are the $3 \times 3$ identity and zero matrices, respectively.

$A= \begin{bmatrix} 2 & 3 & 6 \ 0 & 4 & 4 \ 2 & 0 & 4 \end{bmatrix}$ , so

$A + 2 I = \begin{bmatrix} 2+2 & 3 & 6 \ 0 & 4+2 & 4 \ 2 & 0 & 4+2 \end{bmatrix}$

$= \begin{bmatrix} 4& 3 & 6 \ 0 & 6 & 4 \ 2 &6& 2\end{bmatrix}$

Changing to reduced row echelon form:

$R1 \leftrightarrow R3$

$\begin{bmatrix} 2 &6& 2 \ 0 & 6 & 4 \ 4& 3 & 6 \end{bmatrix}$

$\frac{1}{2} R1 \rightarrow R1$

$\begin{bmatrix} 1 &3&1 \ 0 & 6 & 4 \ 4& 3 & 6 \end{bmatrix}$

$-4R1+ R3 \rightarrow R3$

$\begin{bmatrix} 1 &3&1 \ 0 & 6 & 4 \ 0& -9 & 2 \end{bmatrix}$

$\frac{1}{6} R2 \rightarrow R2$

$\begin{bmatrix} 1 &3&1 \ 0 & 1 & \frac{2}{3} \ 0& -9 & 2 \end{bmatrix}$

$-3R2 + R1 \rightarrow R1$

$9 R2 + R3 \rightarrow R3$

$\begin{bmatrix} 1 &0 &-1 \ 0 & 1 & \frac{2}{3} \ 0& 0& 8 \end{bmatrix}$

$\frac{1}{8} R3 \rightarrow R3$

$\begin{bmatrix} 1 &0 &-1 \ 0 & 1 & \frac{2}{3} \ 0& 0& 1 \end{bmatrix}$

We do not need to go further to see that this matrix will not have a row of zeroes. This means the rank of the matrix is 3, and the nullity is 0. If this happens, the tested value, in this case , is not an eigenvalue.

$\begin{align*}&\text{Approximate }\begin{bmatrix}x\y\end{bmatrix}\&\text{for the system: }\begin{bmatrix}-12&9\13&14\-5&-16\end{bmatrix}\begin{bmatrix}x\y\end{bmatrix}=\begin{bmatrix}-100\-5\14\end{bmatrix}\end{align*}$

$\begin{bmatrix}4.80\-3.63\end{bmatrix}$

$\begin{bmatrix}3.80\-4.63\end{bmatrix}$

$\begin{bmatrix}0.80\-7.63\end{bmatrix}$

$\begin{bmatrix}12.80\4.37\end{bmatrix}$

Explanation

$\begin{align*}&\text{When the rows of a matrix outnumber the columns in an equation,}\&\text{there are a greater number of equations than variables. In order}\&\text{to approximate the values of these variables, a least-squares}\&\text{approach is appropriate. This is done by multiplying each side}\&\text{of the equation by the transpose of the equation matrix, and}\&\text{solving the resulting equation:}\&Ax=B\&A^{T}Ax=A^{T}B\&(A^{T}A)^{-1}(A^{T}A)x=(A^{T}A)^{-1}A^{T}B\&x=(A^{T}A)^{-1}A^{T}B\&\text{Using this, we can approximate our values:}\&\begin{bmatrix}-12&13&-5\9&14&-16\end{bmatrix}\begin{bmatrix}-12&9\13&14\-5&-16\end{bmatrix}\begin{bmatrix}x\y\end{bmatrix}=\begin{bmatrix}-12&13&-5\9&14&-16\end{bmatrix}\begin{bmatrix}-100\-5\14\end{bmatrix}\&\begin{bmatrix}338&154\154&533\end{bmatrix}\begin{bmatrix}x\y\end{bmatrix}=\begin{bmatrix}1065\-1194\end{bmatrix}\&\begin{bmatrix}x\y\end{bmatrix}=\begin{bmatrix}4.80\-3.63\end{bmatrix}\end{align*}$