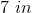Kites
Help Questions
ISEE Upper Level Quantitative Reasoning › Kites
Two diagonals of a kite have the lengths of 

Explanation
The area of a kite is half the product of the diagonals, i.e.
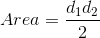
where 

Two diagonals of a kite have the lengths of 

Explanation
The area of a kite is half the product of the diagonals, i.e.
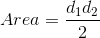
where 

A kite has the area of 

Explanation
The area of a kite is half the product of the diagonals, i.e.
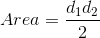
where 

A kite has the area of 

Explanation
The area of a kite is half the product of the diagonals, i.e.
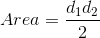
where 

In the following kite, 



Explanation
When you know the length of two unequal sides of a kite and their included angle, the following formula can be used to find the area of a kite:

where _


In the following kite, 



Explanation
When you know the length of two unequal sides of a kite and their included angle, the following formula can be used to find the area of a kite:

where _


Find the area of a kite with one diagonal having length 18in and the other diagonal having a length that is half the first diagonal.
Explanation
To find the area of a kite, we will use the following formula:
where p and q are the lengths of the diagonals of the kite.
Now, we know the length of one diagonal is 18in. We also know the other diagonal is half of the first diagonal. Therefore, the second diagonal has a length of 9in.
Knowing this, we can substitute into the formula. We get
Find the area of a kite with one diagonal having length 18in and the other diagonal having a length that is half the first diagonal.
Explanation
To find the area of a kite, we will use the following formula:
where p and q are the lengths of the diagonals of the kite.
Now, we know the length of one diagonal is 18in. We also know the other diagonal is half of the first diagonal. Therefore, the second diagonal has a length of 9in.
Knowing this, we can substitute into the formula. We get
Cassie is making a kite for her little brother. She has two plastic tubes to use as the skeleton, measuring 

Explanation
To find the area of a kite, use the formula 


Since Cassie has one tube measuring 




Cassie is making a kite for her little brother. She has two plastic tubes to use as the skeleton, measuring 

Explanation
To find the area of a kite, use the formula 


Since Cassie has one tube measuring