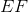Triangles
Help Questions
ISEE Upper Level Quantitative Reasoning › Triangles
The lengths of the hypotenuses of ten similar right triangles form an arithmetic sequence. The smallest triangle has legs of lengths 5 and 12 inches; the second-smallest triangle has a hypotenuse of length one and one half feet.
Which of the following responses comes closest to the area of the largest triangle?
4 square feet
3 square feet
5 square feet
6 square feet
7 square feet
Explanation
The hypotenuse of the smallest triangle can be calculated using the Pythagorean Theorem:

Let 


The arithmetic sequence formula is
The length of the hypotenuse of the largest triangle - the tenth triangle - can be found by substituting 

The largest triangle has hypotenuse of length 58 inches. Since the triangles are similar, corresponding sides are in proportion. If we let 

Similarly,
The area of a right triangle is half the product of its legs:

Divide this by 144 to convert to square feet:
Of the given responses, 4 square feet is the closest, and is the correct choice.



Which is the greater quantity?
(a) The perimeter of
(b) The perimeter of
It is impossible to tell from the information given.
(a) and (b) are equal.
(a) is greater.
(b) is greater.
Explanation
No information is given about the legs of either triangle; therefore, no information about their perimeters can be deduced.

The above diagram depicts trapezoid 
(a)
(b)
(a) and (b) are equal.
(a) is greater.
(b) is greater.
It is impossible to tell from the information given.
Explanation





The Same-Side Interior Angles Theorem states that if two parallel lines are crossed by a transversal, then the sum of the measures of a pair of same-side interior angles is always 
Therefore, 

Refer to the above figure. The shaded region is a semicircle with area 

Explanation
Given the radius 

Substituting 
The diameter of this semicircle is twice this, which is 




Which is the greater quantity?
(a) The sum of the measures of the exterior angles of a thirty-sided polygon, one per vertex
(b) The sum of the measures of the exterior angles of a forty-sided polygon, one per vertex
(a) and (b) are equal
It is impossible to tell from the information given
(a) is greater
(b) is greater
Explanation
The Polygon Exterior-Angle Theorem states that the sum of the measures of the exterior angles of any polygon, one per vertex, is 

Refer to the above figure. The shaded region is a semicircle with area 

Explanation
Given the radius 

Substituting 
The diameter of this semicircle is twice this, which is 




A hexagon has six angles with measures
Which quantity is greater?
(a)
(b) 240
(a) and (b) are equal
(a) is greater
(b) is greater
It is impossible to tell from the information given
Explanation
The angles of a hexagon measure a total of 
The quantities are equal.
Given Trapezoid 

Which is the greater quantity?
(a)
(b)
(a) is greater
(b) is greater
(a) and (b) are equal
It is impossible to tell from the information given
Explanation




The Same-Side Interior Angles Theorem states that if two parallel lines are crossed by a transversal, then the sum of the measures of a pair of same-side interior angles is always 


Substitute:
(a) is the greater quantity





Which is the greater quantity?
(a)
(b)
(a) is greater.
(b) is greater.
(a) and (b) are equal.
It is impossible to tell from the information given.
Explanation
Each right triangle is a 
Since 



By the 



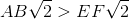
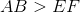
The lengths of the hypotenuses of ten similar right triangles form an arithmetic sequence. The smallest triangle has legs of lengths 5 and 12 inches; the second-smallest triangle has a hypotenuse of length one and one half feet.
Which of the following responses comes closest to the area of the largest triangle?
4 square feet
3 square feet
5 square feet
6 square feet
7 square feet
Explanation
The hypotenuse of the smallest triangle can be calculated using the Pythagorean Theorem:

Let 


The arithmetic sequence formula is
The length of the hypotenuse of the largest triangle - the tenth triangle - can be found by substituting 

The largest triangle has hypotenuse of length 58 inches. Since the triangles are similar, corresponding sides are in proportion. If we let 

Similarly,
The area of a right triangle is half the product of its legs:

Divide this by 144 to convert to square feet:
Of the given responses, 4 square feet is the closest, and is the correct choice.