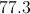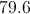Mean
Help Questions
ISEE Middle Level Quantitative Reasoning › Mean
Find the mean of the data set provided:

Explanation
In order to answer this question correctly, we need to recall the definition of mean:
Mean: The mean of a data set is the average of the numbers in a data set.
In order to calculate the mean we must first add up all of the numbers in the data set:
Next, we need to divide by the number of addends, or the number of numbers in the data set:
The mean for this data set is
Find the mean of the data set provided:

Explanation
In order to answer this question correctly, we need to recall the definition of mean:
Mean: The mean of a data set is the average of the numbers in a data set.
In order to calculate the mean we must first add up all of the numbers in the data set:
Next, we need to divide by the number of addends, or the number of numbers in the data set:
The mean for this data set is
Give the mean of the data set (nearest tenth, if applicable):
Explanation
Add the six elements and divide the sum by 6:
Give the mean of the data set (nearest tenth, if applicable):
Explanation
Add the six elements and divide the sum by 6:
Using the information given in each question, compare the quantity in Column A to the quantity in Column B.
Allie has scored 79, 77, 96, 71, 85, 86, 90, and 84 on her eight science quizzes, and her teacher drops the highest and lowest score.
Column A Column B
Allie's quiz average Allie's quiz average
before the dropped scores after the dropped scores
The two quantities are equal.
The quantity in Column A is greater.
The quantity in Column B is greater.
The relationship cannot be determined from the information given.
Explanation
Add up the 8 test scores and divide by 8 to figure out the mean (83.5). Now figure out the average between the highest and lowest scores
Since the dropped tests have the same average as the original 8 tests, Allie's score would not change. The correct answer is that the two columns are equal.
Note: If you are good at mental math, here is a quick way to figure out the average of the 8 tests:
First, estimate the average (say, 80). Next, go through the numbers and add or subtract the difference between the number and 80.
79 is 1 below 80.
77 is 3 below 80 (so now we're 4 below 80).
As we continue through the numbers, we get
12 above, 3 above, 8 above, 14 above, 24 above, 28 above.
So the 8 scores are cumulatively 28 above an average score of 80. Now, simply divide 28 by 8 and add this to 80.
Find the mean of the following set of numbers:
46.7
43
54.5
40.9
Explanation
The mean is equal to the sum of the values divided by the total number of values.
Find the mean of the following set of numbers:
46.7
43
54.5
40.9
Explanation
The mean is equal to the sum of the values divided by the total number of values.
Using the information given in each question, compare the quantity in Column A to the quantity in Column B.
Allie has scored 79, 77, 96, 71, 85, 86, 90, and 84 on her eight science quizzes, and her teacher drops the highest and lowest score.
Column A Column B
Allie's quiz average Allie's quiz average
before the dropped scores after the dropped scores
The two quantities are equal.
The quantity in Column A is greater.
The quantity in Column B is greater.
The relationship cannot be determined from the information given.
Explanation
Add up the 8 test scores and divide by 8 to figure out the mean (83.5). Now figure out the average between the highest and lowest scores
Since the dropped tests have the same average as the original 8 tests, Allie's score would not change. The correct answer is that the two columns are equal.
Note: If you are good at mental math, here is a quick way to figure out the average of the 8 tests:
First, estimate the average (say, 80). Next, go through the numbers and add or subtract the difference between the number and 80.
79 is 1 below 80.
77 is 3 below 80 (so now we're 4 below 80).
As we continue through the numbers, we get
12 above, 3 above, 8 above, 14 above, 24 above, 28 above.
So the 8 scores are cumulatively 28 above an average score of 80. Now, simply divide 28 by 8 and add this to 80.
Find the mean in this set of numbers:
Explanation
First, add all the numbers in this set:
Then, divide by 5:
Answer: The mean is 594.
Find the mean of the following set of numbers:
Explanation
To solve, simply add them all up and divide by their total.
Thus,