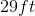How to find the area of a parallelogram
Help Questions
ISEE Lower Level Quantitative Reasoning › How to find the area of a parallelogram
Annie has a piece of wallpaper that is 

Explanation
This problem asks us to calculate the amount of space that the wallpaper will cover. The amount of space that something covers can be described as its area. In this case area is calculated by using the formula
What is the length of a rectangular room with a perimeter of 
Explanation
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
Explanation
The fence is going around the garden, so this is a perimeter problem.
What area of the rectangle is filled in?

Explanation
Area is the amount of space within the perimeter of a two-dimensional shape. The rectangle is split into 


What is the length of a rectangular room with a perimeter of 
Explanation
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Joe has a piece of wallpaper that is 

Explanation
This problem asks us to calculate the amount of space that the wallpaper will cover. The amount of space that something covers can be described as its area. In this case area is calculated by using the formula
What is the length of a rectangular room with a perimeter of 
Explanation
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
What is the length of a yard with a perimeter of 
Explanation
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
David wants to put a fence around his backyard. How much fencing will he need if his backyard is 
Explanation
The fence is going around the backyard, so this is a perimeter problem.
What is the length of a yard with a perimeter of 
Explanation
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide