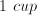ISEE Lower Level Quantitative Reasoning - Ratio and Proportion

A foot tree casts a shadow of feet. How long is the shadow of a nearby foot tall building if the tree and its shadow are in the same ratio as the building and its shadow?

Explanation

To solve this, I need to set up a proportion, and then solve algebraically.

feet, the height of the tree, is equivalent in our proportion to feet, the building's height.

feet, the tree's shadow, is equivalent in our proportion to , the building's shadow.

$\frac{30}{20}=\frac{300}{x}$

Cross-multiply:

Divide each side by :

Scott's mother bakes 12 cookies and he eats half of them. Scott's mom then puts red frosting on 4 cookies and blue frosting on the rest of the cookies. What is the ratio of cookies with red frosting to cookies with blue frosting?

Explanation

If Scott's mother bakes 12 cookies and he eats half of them, that means he will eat 6 cookies, leaving 6 uneaten cookies.

If Scott's mom then puts red frosting on 4 cookies and blue frosting on the rest of the cookies, 2 cookies will get blue frosting. ().

Therefore, the ratio of cookies with red frosting to cookies with blue frosting is , which is equal to .

There are students in a fifth grade class. If there are girls in the class, what is the ratio of the number of boys in the class to the total number of students in the class?

$\frac{2}{3}$

$\frac{3}{2}$

$\frac{7}{8}$

$\frac{3}{4}$

Explanation

First, find the number of boys in the class by subtracting the number of girls in the class from the total number of students.

$\text{Number of boys}=36-12=24$

Now, we know that the ratio of the number of boys in the class to the total number of students in the class is $24\text{ to }36$ .

We can express that ratio as the following fraction:

$\frac{24}{36}=\frac{2}{3}$

A recipe calls for $\dpi{100} \frac{2}{3}$ of a cup of flour and $\dpi{100} \frac{2}{3}$ of a cup of sugar. How many cups of sugar and flour combined does the recipe call for?

$\dpi{100} 1\frac{1}{3}\ cups$

$\dpi{100} 1\frac{2}{3}\ cups$

$\dpi{100} 2\ cups$

$\dpi{100} 1\ cup$

Explanation

Add $\dpi{100} \frac{2}{3}+\frac{2}{3}$ .

Since both of these fractions have the same denominator, we just rewrite 3 on the bottom. When you add fractions, then add straight across the top, $\dpi{100} 2+2=4$ .

This gives us $\dpi{100} \frac{4}{3}$ .

We can turn this into a mixed number by dividing $\dpi{100} 4\div 3=1$ with a remainder of 1. We place the orginal one as our whole number, and the remainder over the 3 for the fraction, $\dpi{100} 1\frac{1}{3}$ .

Stacy has started collecting coins. She has twice as many wheat pennies as she does 1946 dimes, and three times as many 1983 quarters as she does 1946 dimes. If Stacy has $\small 4$ 1946 dimes, what is the ratio of wheat pennies to 1983 quarters?

$\small 2:3$

$\small 8:12$

$\small 12:4$

$\small 12:8$

$\small 4:3$

Explanation

We know that Stacy has $\small 4$ 1946 dimes.

We also know that she has twice as many wheat pennies, so we must multiply $\small 4$ by $\small 2$ to find the total number of wheat pennies.

$\small 4\cdot 2=8$

We also know that Stacy has three times as many 1986 quarters, so we multiply $\small 4$ by $\small 3$ to find the total number of 1986 quarters.

$\small 4\cdot 3=12$

Now our ratio of wheat pennies to 1986 quarters is $\small 8:12$ , but this can be simplified because both numbers are divisible by $\small 4$ .

$\small (8/4)=2$

$\small (12/4)=3$

So our ratio becomes $\small 2:3$

For every 3 peanuts in a bag of trail mix, there are 1 chocolate chip and 2 raisins. What is the proportion of raisins in the mix?

$\frac{1}{3}$

$\frac{2}{5}$

$\frac{1}{2}$

$\frac{1}{4}$

Explanation

Given that there are 3 peanuts for every 1 chocolate chip and 2 raisins, the proportion of raisins can be found by dividing the number of raisins by the sum of all the items in the mix. This results in:

$\frac{2}{3+1+2}=\frac{2}{6}=\frac{1}{3}$ .

Therefore, $\frac{1}{3}$ is the correct answer.

Stacy has started collecting coins. She has twice as many wheat pennies as she does dimes, and three times as many quarters as she does dimes. If Stacy has $\small 4$ dimes, what is the ratio of wheat pennies to quarters?

$\small 2:3$

$\small 8:12$

$\small 12:4$

$\small 12:8$

$\small 4:3$

Explanation

We know that Stacy has $\small 4$ 1946 dimes.

We also know that she has twice as many wheat pennies, so we must multiply $\small 4$ by $\small 2$ to find the total number of wheat pennies.

$\small 4\cdot 2=8$

We also know that Stacy has three times as many 1986 quarters, so we multiply $\small 4$ by $\small 3$ to find the total number of 1986 quarters.

$\small 4\cdot 3=12$

Now our ratio of wheat pennies to 1986 quarters is $\small 8:12$ , but this can be simplified because both numbers are divisible by $\small 4$ .

$\small (8/4)=2$

$\small (12/4)=3$

So our ratio becomes $\small 2:3$

Find an equivalent ratio.

Explanation

An equivalent ratio of is .

This is the furthest simplification of the ratio.
The greatest common divisor is needed to simplify the expression.

Both and are divisible by , $\frac{15}{3}=5$ and $\frac{3}{3}=1$ .

Thus, the correct answer is .

There are 18 tea bags in a box. Beth uses 2 tea bags, Brad uses 1 tea bag, and Joe uses 1 tea bag. What fraction of the tea bags now remain?

$\frac{7}{9}$

$\frac{14}{9}$

$\frac{2}{9}$

$\frac{15}{18}$

Explanation

If there are 18 tea bags in a box and Beth uses 2 tea bags, Brad uses 1 tea bag, and Joe uses 1 tea bag, then 14 tea bags will remain.

Given that $\frac{14}{18}=\frac{7}{9}$ , the correct answer is $\frac{7}{9}$ .

If Katie's computer has 60% of its power left after being on for 2 hours, how many hours of battery power remain?

Explanation

If Katie's computer has 60% of its power left after being on for 2 hours, then that means 40% of the battery was used to power the 2 hours. X represents the total number of hours that the battery can last.

$\frac{40}{100}=\frac{2}{x}$

Next, we divide each side of the equation by 40. This results in:

Since 60% of 5 is equal to 3, the correct answer is 3.

Ratio and Proportion

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation