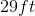Plane Geometry
Help Questions
ISEE Lower Level Quantitative Reasoning › Plane Geometry
What is the area of the right triangle in the following figure?

Explanation
There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

What is the area of the figure below?

Explanation
To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, 


To find our final answer, we need to add the areas together.
A square has an area of 
Explanation
You can find the area of a square by multiplying two sides together. All of the sides of a square are equal. In this case, 
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
Explanation
The fence is going around the garden, so this is a perimeter problem.
What is the area of the rectangle?

Explanation
The formula to find area is 
*Area is the number of square units inside a shape, which is why area is always written with square units.
What is the area of the figure below?

Explanation
To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, 


To find our final answer, we need to add the areas together.
What is the area of the figure below?

Explanation
To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, 


To find our final answer, we need to add the areas together.
What is the area of the figure below?

Explanation
To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, 


To find our final answer, we need to add the areas together.
What is the area of the figure below?

Explanation
To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, 


To find our final answer, we need to add the areas together.
What is the area of the figure below?

Explanation
To find the area of the figure above, we need to slip the figure into two rectangles.

Using our area formula, 


To find our final answer, we need to add the areas together.