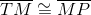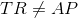From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

Next, use this value to find the area of the trapezoid.

Plug in the given and found values to find the area.

Next, find the area of the triangle.

To find the area of the figure, add the two areas together.

Make sure to round to places after the decimal.

To find the perimeter of this trapezoid, first find the length of the larger base. Then, find the sum of all of the sides. It's important to note that since this is an isosceles trapezoid, both of the non-parallel sides will have the same length.

The solution is:

The smaller base is equal to inches. Thus, the larger base is equal to:

, where the length of one of the non-parallel sides of the isosceles trapezoid.

A trapezoid is a four-sided shape with straight sides that has a pair of opposite parallel sides. The other sides may or may not be parallel. A square and a rectangle are both considered trapezoids.

The formula to find the area of a trapezoid is

.

Substitute in the values for the area, a base, and the height. Then solve for .

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

Next, use this value to find the area of the trapezoid.

Plug in the given and found values to find the area.

Next, find the area of the triangle.

To find the area of the figure, add the two areas together.

Make sure to round to places after the decimal.

To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one Base two (leg), where the length of "leg" is one of the two equivalent nonparallel sides.

Thus, the solution is:

Check the solution by plugging in the answer:

To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one Base two (leg), where the length of "leg" is one of the two equivalent nonparallel sides.

Thus, the solution is:

Check the solution by plugging in the answer:

The fact that the trapezoid is isosceles is actually irrelevant. Since and are the midpoints of legs and , it holds by definition that

and

It follows that

However, the bases of each trapezoid are noncongruent, by definition, so, in particular,

Assume that 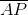is the longer base - this argument works symmetrically if the opposite is true. Let - equivalently, .

Since the bases are of unequal length, . The length of the midsegment is the arithmetic mean of the lengths of these two bases, so

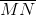
Since , it follows that

,

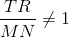
and

.

This disproves similarity, since one condition is that corresponding sides must be in proportion.

In a trapezoid, the angles on the same leg (called adjacent angles) are supplementary, meaning they add up to degrees.

and the angle measuring degrees are adjacent angles that are supplementary.

To find the perimeter of this trapezoid, first find the length of the larger base. Then, find the sum of all of the sides. It's important to note that since this is an isosceles trapezoid, both of the non-parallel sides will have the same length.

The solution is:

The smaller base is equal to inches. Thus, the larger base is equal to:

, where the length of one of the non-parallel sides of the isosceles trapezoid.