How to find the height of an equilateral triangle
Help Questions
Geometry › How to find the height of an equilateral triangle
Find the height of an equilateral triangle with a side length of 
Explanation
An equilateral triangle has three equal sides, as can be deduced from its name. This also means that as a result, the triangle is also equiangular. That is, all its interior angles are the same. Because the sum of internal angles of a triangle is 

The height (the dotted line in the diagram) is the length that bisects the apical angle while bisecting the base of the triangle. Drawing the dotted line splits the equilateral triangle into two congruent right triangles. Because they're the same, we only need to consider one of the two smaller triangles to obtain our answer. Keeping in mind that the base of the equilateral triangle has been bisected, this means that the base of the right triangle has the length of 


This problem can also be solved using trigonometric functions or even revisiting 30-60-90 triangle rules.
Using the Pythagorean Theorem,
Therefore, the height of the equilateral triangle is 
If an equilateral triangle has a length of 
Explanation
The following formula can be used to determine the height of an equilateral triangle when we are given the length of the sides:
The equilateral triangle shown below has a side length of 

Explanation
To solve for the height of an equilateral triangle, we can divide the triangle into two right triangles. In the below image, the bisecting line represents the height, and we can solve for height by applying the Pythagorean Theorem:
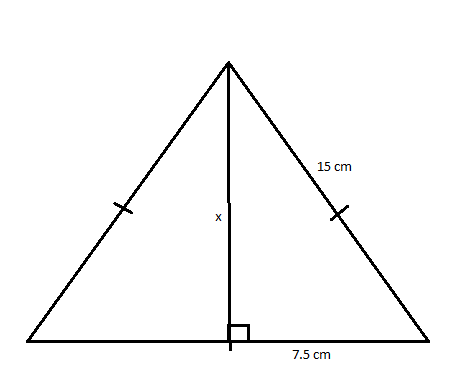
What is the height of an equilateral triangle with a side length of 8 in?
Explanation
An equilateral triangle has three congruent sides, and is also an equiangular triangle with three congruent angles that each meansure 60 degrees.
To find the height we divide the triangle into two special 30 - 60 - 90 right triangles by drawing a line from one corner to the center of the opposite side. This segment will be the height, and will be opposite from one of the 60 degree angles and adjacent to a 30 degree angle. The special right triangle gives side ratios of 



The side with length 

ΔABC is an equilateral triangle with side of length 8.
Find the height (to the nearest tenth).
6.9
7.1
7.3
7.5
6.7
Explanation
Equilateral triangles have sides of equal length, with angles of 60°. To find the height, we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles.
Now, the side of the original equilateral triangle (lets call it "a") is the hypotenuse of the 30-60-90 triangle. Because the 30-60-90 triange is a special triangle, we know that the sides are x, x
Thus, a = 2x and x = a/2.
Height of the equilateral triangle =
ΔABC is an equilateral triangle with side 12.
Find the height of ΔABC (to the nearest tenth).
10.4
10.6
10.2
10.0
9.8
Explanation
Equilateral triangles have sides of all equal length and angles of 60°. To find the height, we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles.
Now, the side of the original equilateral triangle (lets call it "a") is the hypotenuse of the 30-60-90 triangle. Because the 30-60-90 triange is a special triangle, we know that the sides are x, x
Thus, a = 2x and x = a/2.
Height of the equilateral triangle =
What is the height of a triangle with side lengths 4, 4, 4?
Explanation
To solve, it's easiest to first visualize the height's relationship with the rest of the triangle's sides:
The height is one of the legs of a right triangle. The hypotenuse is 4, and the other leg is 2, or half of the base side, 4. To determine the height, use Pythagorean Theorem:












































