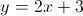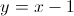How to find the equation of a line
Help Questions
Geometry › How to find the equation of a line
If the 



Explanation
If the y-intercept of a line is 



If the 




Use the following formula for slope and the two points to determine the slope:
Use the slope intercept form and one of the points, suppose 


Therefore, the equation of this line is 
Write the equation for the line passing through the points 
Explanation
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Find the equation of a line that goes through the points 

Explanation
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 


Refer to the above figures. To the left is the graph of the equation
What inequality is graphed at right?
Explanation
As indicated by the solid line, the graph of the inequality at right includes the line of the equation, so the inequality graphed is either
or
To determine which one, we can select a test point and substitute its coordinates in either inequality, testing whether it is true for those values. The easiest test point is 




Refer to the above diagrams. At left is the graph of the equation
At right is the graph of the equation
Which of the following is a graph of the system of linear inequalities




Explanation
The graph of a linear inequality that includes either the 


This is true; select the side of this line that includes the origin.
This is false; select the side of this line that does not include the origin.
The solution sets of the individual inequalities are below:

The graph of the system is the intersection of the two sets, shown below:


Which of the following inequalities is graphed above?
Explanation
The boundary line is a horizontal line which has 


The inequality is either 


Find the equation of a line that goes through the points 

Explanation
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
Find the equation for a line passing through the points 

Explanation
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Find the equation of a line that goes through the points 

Explanation
Recall that the slope-intercept form of a line:

where 

First, find the slope of the line by using the following formula:
Next, find the y-intercept of the line by plugging in 
Plugging in 
Solve for 
The equation of the line is then 
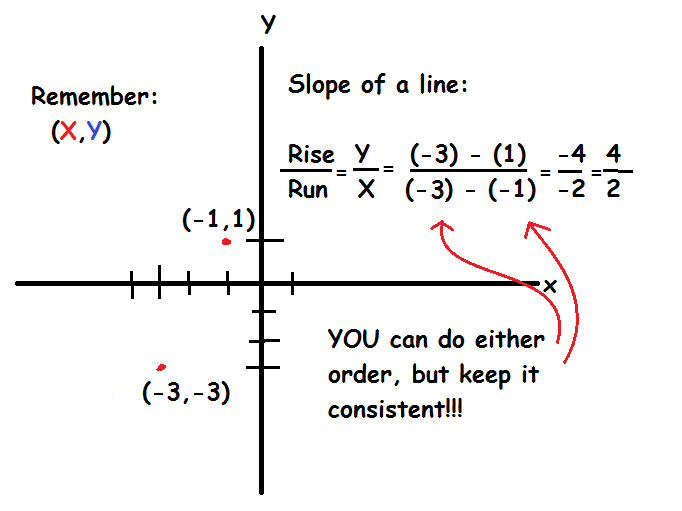
Given two points 

Explanation
If we have two points, we can find the slope of the line between them by using the definition of the slope:

Now that we have our slope ( 




In order to find the y-intercept, we simply plug in one of the points on our line
So our equation looks like