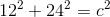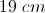How to find the diagonal of a prism
Help Questions
Geometry › How to find the diagonal of a prism
A right rectangular prism has a width of 


None of the other answers.
Explanation
To find the diagonal distance of a prism, you can use the formula:




So, in this problem


The above cube has edges of length 1. True or false: The dashed line has length 
False
True
Explanation
Examine the diagram below.










A right rectangular prism has a height of 


None of the other answers.
Explanation
First, given the volume, you need to find the width and length. The volume of a right, rectangular prism can be found using




Solving for 
So, the width of the prism is 3 feet.
Remember that the length is twice the width, so the length is 6 feet.
Now you may use the formula for finding the diagonal:


A right, rectangular prism has a length of 



None of the other answers.
Explanation
First, use the volume formula,

Since 

Now you can plug in the length, width and height into the formula for finding the diagonal of the prism.

The surface area of a right, rectangular prism is 


None of the other choices.
Explanation
Use the surface area, 280 square inches, and the formula for finding the surface area of a right, rectangular prsim 
So,
Since 

So, the width of the figure is 2 inches and the length is 10 inches.
Now, use the formula for finding the diagonal of a right, rectangular prism:

A right, rectangular prism has a surface area of 
None of the other answers.
Explanation
Use the surface area of the prism to find the missing length, width and height.
So, the prism's length is 1 meter, the width is 2 meters and the height is 4 meters.
Now you can find the diagonal distance using those values.

Find the diagonal of the prism. The diagonal is represented by the dashed line.
Explanation
The length of the diagonal is from the bottom left hand corner closest to us to the top right hand corner that's farthest away from us.
This kind of a problem may seem to be a little more complicated than it really is.
In order to solve for the diagonal length, all that's required is the Pythagorean Theorem. This equation will be used twice to solve for the dashed line.
For the first step of this problem, it's helpful to imagine a triangle "slice" that's being taken inside the prism.

We can already "map out" that D2 (the hypotenuse of the dashed triangle) can be solved by using the Pythagorean Theorem if we can obtain the length of the other leg (D1).
The next step of this problem is to solve for D1. This will be the first use of the Pythagorean theorem. D1 is the diagonal of the base and is limited to a 2D face. This can be represented as:
The hypotenuse of the base, or the mystery length leg of the dashed triangle, can be solved by using the Pythagorean Theorem:
Now that we calculated the length of D1, D2 can be solved for by using the Pythagorean Theorem a second time:
A right, rectangular prism has a volume of 

None of the other answers.
Explanation
First, use the volume to find the missing height and length.
Since the length is three times the height, use 

So, 
So the height of the prism is 2 centimeters, and the length is 6 centimeters.
Use these values to now solve for the diagonal distance.

What is the length of the diagonal of a rectangular box with the dimensions of 
Explanation
To solve this problem we need an extension of the Pythagorean Theorem:
So the equation to solve becomes
So the distance of the diagonal is