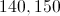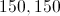How to find an angle in a pentagon
Help Questions
Geometry › How to find an angle in a pentagon
Let the area of a regular pentagon be 
Explanation
Area has no effect on the value of the interior angles of a pentagon. To find the sum of all angles of a pentagon, use the following formula, where 
There are 5 sides in a pentagon.
Divide this number by 5 to determine the value of each angle.
True or false: Each of the exterior angles of a regular pentagon measures 
True
False
Explanation
If one exterior angle is taken at each vertex of any polygon, and their measures are added, the sum is 

Solve for 
The statement is true.
What is the sum of three angles in a hexagon if the perimeter of the hexagon is 
Explanation
The perimeter in this question is irrelevant. Use the interior angle formula to determine the total sum of the angles in a hexagon.
There are six interior angles in a hexagon.
Each angle will be a sixth of the total angle.
Therefore, the sum of three angles in a hexagon is:
Given: Pentagon 
True, false, or undetermined: Pentagon 
Undetermined
True
False
Explanation
Suppose Pentagon 

A pentagon has 5 sides, so set 
Since one angle is given to be of measure 
Add four interior angles in a regular pentagon. What is the result?
Explanation
Use the interior angle formula to find the total sum of angles in a pentagon.

Divide this number by 5, since there are five interior angles.
The sum of four interior angles in a regular pentagon is:
Suppose an interior angle of a regular pentagon is 

Explanation
The pentagon has 5 sides. To find the value of the interior angle of a pentagon, use the following formula to find the sum of all interior angles.
Substitute 
Divide this number by 5 to determine the value of each interior angle.
Every interior angle is 108 degrees. The problem states that an interior angle is 

What is the sum of two interior angles of a regular pentagon if the perimeter is 6?
Explanation
The perimeter of a regular pentagon has no effect on the interior angles of the pentagon.
Use the following formula to solve for the sum of all interior angles in the pentagon.
Since there are 5 sides in a pentagon, substitute the side length 
Divide this by 5 to determine the value of each angle, and then multiply by 2 to determine the sum of 2 interior angles.
The sum of 2 interior angles of a pentagon is 
True or false: Each of the five angles of a regular pentagon measures 
False
True
Explanation
A regular polygon with 

Setting 
The statement is therefore false.
The angles at 3 verticies of a pentagon are 60, 80 and 100. Which of the following could NOT be the measures of the other 2 angles?
Explanation
The sum of the angles in a polygon is
For a pentagon, this equals 540. Since the first 3 angles add up to 240, the remaining 2 angles must add up to