Properties of polygons and circles
Help Questions
HiSET › Properties of polygons and circles
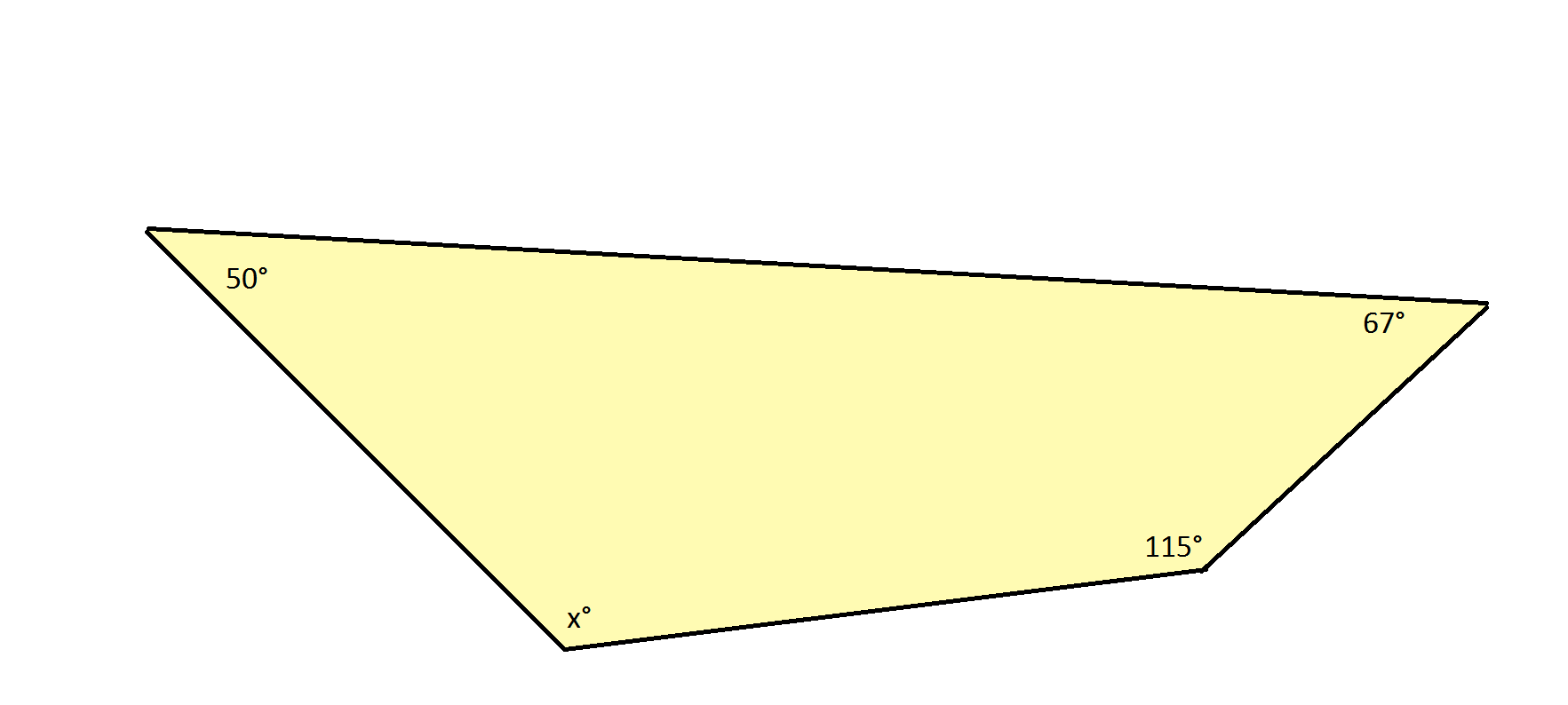
A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.
Explanation
The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:


For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:
Solving for 
Solving for 

The depicted circle has a radius of 3 cm. The arc length between the two points shown on the circle is 
Explanation
First, find the area and circumference of the circle using the radius and the following formulae for circles:
Substituting in 3 for 
Next, find what fraction of the total circumference is between the two points on the circle (the arc length).
Finally, use this fraction to calculate the area of the enclosed sector. Note that this area is proportional to the above fraction. In other words:
So the Sector Area is one sixth of the total area.
Cross multiply:
Divide both sides by 6, then simplify to get the final answer:

The depicted circle has a radius of 3 cm. The arc length between the two points shown on the circle is 
Explanation
First, find the area and circumference of the circle using the radius and the following formulae for circles:
Substituting in 3 for 
Next, find what fraction of the total circumference is between the two points on the circle (the arc length).
Finally, use this fraction to calculate the area of the enclosed sector. Note that this area is proportional to the above fraction. In other words:
So the Sector Area is one sixth of the total area.
Cross multiply:
Divide both sides by 6, then simplify to get the final answer:

A quadrilateral is shown, and the angle measures of 3 interior angles are given. Find x, the missing angle measure.
Explanation
The sum of the measures of the interior angles of a quadrilateral is 360 degrees. The sum of the measures of the interior angles of any polygon can be determined using the following formula:


For example, with a quadrilateral, which has 4 sides, you obtain the following calculation:
Solving for 
Solving for 
Give the perimeter of a regular octagon in yards if the length of each side is 





Explanation
The perimeter of a regular octagon - the sum of the lengths of its (eight congruent) sides - is eight times the common sidelength, so the perimeter of the octagon is 

Give the perimeter of a regular octagon in yards if the length of each side is 





Explanation
The perimeter of a regular octagon - the sum of the lengths of its (eight congruent) sides - is eight times the common sidelength, so the perimeter of the octagon is 


Refer to the above figure. Give the ratio of the area of Sector 2 to that of Sector 1.
Explanation
The ratio of the area of the larger Sector 2 to that of smaller Sector 1 is equal to the ratio of their respective arc measures - that is,

Therefore, it is sufficient to find these arc measures.
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Add 360 to both sides:
Divide both sides by 2:

the degree measure of 
It follows that
By the Arc Addition Principle,
Since 



and
The ratio 

a 5 to 1 ratio.




Evaluate 
Explanation






Substitute and solve for 


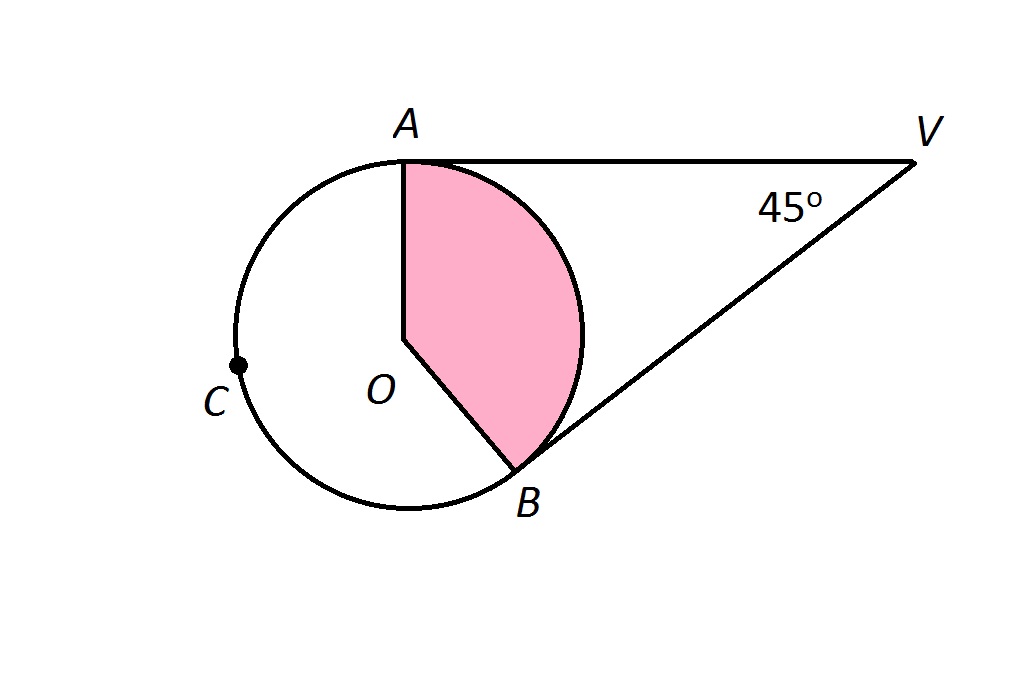


Explanation



Therefore, we need to find 
If the sides of an angle with vertex outside the circle are both tangent to the circle, the angle formed is half the difference of the measures of the arcs. Therefore,
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the measure of 





Explanation
The radius of the circle is given to be 



The length 

Thus, it is first necessary to find the degree measure of 
Letting 
We are also given that
Making substitutions, and solving for 
Multiply both sides by 2:
Subtract 360 from both sides:
Divide both sides by 

the degree measure of 
Thus, the length 





























































































