Equilateral Triangles
Help Questions
Math › Equilateral Triangles
Triangle A: A right triangle with sides length 

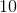
Triangle B: An equilateral triangle with side lengths 
Which triangle has a greater area?
Triangle B
Triangle A
The areas of the two triangles are the same.
There is not enough information given to determine which triangle has a greater area.
Explanation
The formula for the area of a right triangle is 


The formula for the area of an equilateral triangle is 

To determine which of the two areas is greater without using a calculator, rewrite the areas of the two triangles with comparable factors. Triangle A's area can be expressed as 



What is the height of an equilateral triangle with side 6?
Explanation
When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the 

What is the height of an equilateral triangle with side 6?
Explanation
When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the 

Triangle A: A right triangle with sides length 

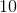
Triangle B: An equilateral triangle with side lengths 
Which triangle has a greater area?
Triangle B
Triangle A
The areas of the two triangles are the same.
There is not enough information given to determine which triangle has a greater area.
Explanation
The formula for the area of a right triangle is 


The formula for the area of an equilateral triangle is 

To determine which of the two areas is greater without using a calculator, rewrite the areas of the two triangles with comparable factors. Triangle A's area can be expressed as 



Find the area of an equilateral triangle whose perimeter is
Explanation
The formula for the perimeter of an equilateral triangle is:
Plugging in our values, we get
The formula for the area of an equilateral triangle is:
Plugging in our values, we get
What is the area of an equilateral triangle with side 11?
Explanation
Since the area of a triangle is
you need to find the height of the triangle first. Because of the 30-60-90 relationship, you can determine that the height is 
Then, multiply that by the base (11).
Finally, divide it by two to get 52.4.
Solve for the value of X in the following equilateral triangle:
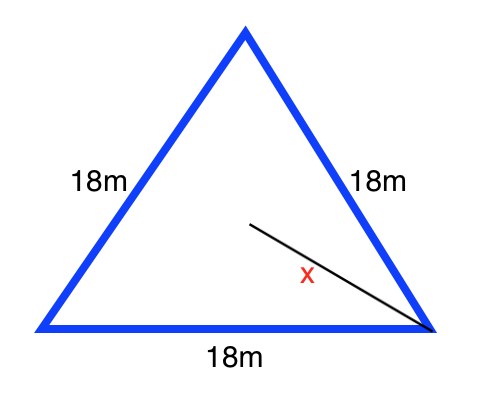
Explanation
If we draw a line segment between X and the base of the triangle, we form a 
We can use the relationships between the sides of a 
We know the base opposite the 

The value of the height opposite the 


Therefore, the value of X will be twice the value of the height:
Solve for the value of X in the following equilateral triangle:

Explanation
If we draw a line segment between X and the base of the triangle, we form a 
We can use the relationships between the sides of a 
We know the base opposite the 

The value of the height opposite the 


Therefore, the value of X will be twice the value of the height:
Find the area of an equilateral triangle whose perimeter is
Explanation
The formula for the perimeter of an equilateral triangle is:
Plugging in our values, we get
The formula for the area of an equilateral triangle is:
Plugging in our values, we get
What is the area of an equilateral triangle with side 11?
Explanation
Since the area of a triangle is
you need to find the height of the triangle first. Because of the 30-60-90 relationship, you can determine that the height is 
Then, multiply that by the base (11).
Finally, divide it by two to get 52.4.
































