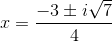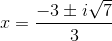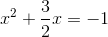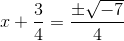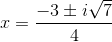Quadratic Equations and Inequalities
Help Questions
Math › Quadratic Equations and Inequalities
Solve the following quadratic inequality:
Explanation
Factor and solve. Since the sign is less than or equal to, we know the inequality will be OR, not AND.

Solve the following quadratic inequality:
Explanation
Factor and solve. Since the sign is less than or equal to, we know the inequality will be OR, not AND.

Solve using the quadratic formula:
Explanation
Use the quadratic formula to solve:
Complete the square:
Explanation
Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Find the sum of the solutions to:
Explanation
Multiply both sides of the equation by 
This can be factored into the form
So we must solve
and
to get the solutions.
The solutions are:
and their sum is 
Complete the square:
Explanation
Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify:
Find the sum of the solutions to:
Explanation
Multiply both sides of the equation by 
This can be factored into the form
So we must solve
and
to get the solutions.
The solutions are:
and their sum is 
Find the sum of the solutions to:
Explanation
Multiply both sides of the equation by 
This can be factored into the form
So we must solve
and
to get the solutions.
The solutions are:
and their sum is 
Solve using the quadratic formula:
Explanation
Use the quadratic formula to solve:
Complete the square:
Explanation
Begin by dividing the equation by 

Square the value in front of the 
Factor the left side of the equation:
Take the square root of both sides and simplify: