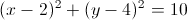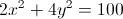Intercepts and Curves
Help Questions
Math › Intercepts and Curves
A straight line passes through the points 

What is the 
Explanation
First calculate the slope:
The standard equation for a line is 
In this equation, 


Plugging in (1,3) we get 
Therefore, 
Our equation for the line is now:
To find the 

Thus, the 
A straight line passes through the points 

What is the 
Explanation
First calculate the slope:
The standard equation for a line is 
In this equation, 


Plugging in (1,3) we get 
Therefore, 
Our equation for the line is now:
To find the 

Thus, the 
What is the x-intercept of 
Explanation
To find the x-intercept, set y equal to zero and solve:
Subtract 
Divide both sides by 
What is the x-intercept of 
Explanation
To find the x-intercept, set y equal to zero and solve:
Subtract 
Divide both sides by 
The center of a circle is 

Explanation
The general equation of a circle is 


Thus, we plug the values given into the above equation to get 
The center of a circle is 

Explanation
The general equation of a circle is 


Thus, we plug the values given into the above equation to get 
Find the 
Explanation
Take out a 





Find the 
Explanation
Take out a 





What is the x-intercept of 
Explanation
To solve for the x-intercept, we set the 

Find the x and y-intercepts of the following equation:
y-intercept:
x-intercept:
y-intercept:
x-intercept:
y-intercept:
x-intercept:
y-intercept:
x-intercept:
y-intercept:
x-intercept:
Explanation
To find the y-intercept, substitute zero for x and solve for y:
The y-intercept is at point 
To find the x-intercept, substitute zero for y and solve for x:
The x-intercept is at point