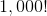Finite Mathematics
Help Questions
Finite Mathematics › Finite Mathematics
The water temperatures in a certain lake over the course of the last seven days are as follows.
Calculate the mean water temperature.
Explanation
To calculate the mean of the water temperatures first recall the formula for mean.
Now substitute in the values from the problem and solve.
Consider the conditional statements:
"If Mickey is a Freemason, then Nelson is a Freemason."
"If Oscar is not a Freemason, then Nelson is not a Freemason."
Nelson is a Freemason. What can be concluded about whether or not Mickey and Oscar are Freemasons?
Oscar is a Freemason; no conclusion can be drawn about Mickey.
Mickey is a Freemason; no conclusion can be drawn about Oscar.
Mickey and Oscar are both Freemasons.
No conclusion can be drawn about either Mickey or Oscar.
Mickey is a Freemason; Oscar is not a Freemason.
Explanation
Consider the second conditional "If Oscar is not a Freemason, then Nelson is not a Freemason.". It is known that Nelson is a Freemason, making the consequent of this conditional false. By a modus tollens argument, it follows that the antecedent is also false, and Oscar is a Freemason.
No conclusion can be drawn about Mickey, however. If Mickey is a Freemason, then by the first conditional, it follows that Nelson is a Freemason, which is already known; if Mickey is not a Freemason, no conclusion can be drawn that is inconsistent with what is known. Thus, either status is consistent with Nelson and Oscar both being Freemasons.
True or false: 
True
False
Explanation









The number of subsets of a set with 



Let 
True or false: 
True
False
Explanation
A set 

Try without a calculator:
Which of the following is equal to 
Explanation
For any whole numbers 

Setting 

Consider the conditional statements:
"If Mickey is a Freemason, then Nelson is a Freemason."
"If Oscar is not a Freemason, then Nelson is not a Freemason."
Nelson is a Freemason. What can be concluded about whether or not Mickey and Oscar are Freemasons?
Oscar is a Freemason; no conclusion can be drawn about Mickey.
Mickey is a Freemason; no conclusion can be drawn about Oscar.
Mickey and Oscar are both Freemasons.
No conclusion can be drawn about either Mickey or Oscar.
Mickey is a Freemason; Oscar is not a Freemason.
Explanation
Consider the second conditional "If Oscar is not a Freemason, then Nelson is not a Freemason.". It is known that Nelson is a Freemason, making the consequent of this conditional false. By a modus tollens argument, it follows that the antecedent is also false, and Oscar is a Freemason.
No conclusion can be drawn about Mickey, however. If Mickey is a Freemason, then by the first conditional, it follows that Nelson is a Freemason, which is already known; if Mickey is not a Freemason, no conclusion can be drawn that is inconsistent with what is known. Thus, either status is consistent with Nelson and Oscar both being Freemasons.
The water temperatures in a certain lake over the course of the last seven days are as follows.
Calculate the mean water temperature.
Explanation
To calculate the mean of the water temperatures first recall the formula for mean.
Now substitute in the values from the problem and solve.
True or false: 
True
False
Explanation









The number of subsets of a set with 



Try without a calculator:
Which of the following is equal to 
Explanation
For any whole numbers 

Setting 

Let 
True or false: 
True
False
Explanation
A set