Functions
Help Questions
8th Grade Math › Functions
Select the equation that best represents a linear function.
Explanation
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
We can add 
This equation is in slope-intercept form; thus, 
Select the equation that best represents a linear function.
Explanation
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
This equation is in slope-intercept form; thus, 
What is the equation of a parabola with vertex 


Explanation
From the vertex, we know that the equation of the parabola will take the form 

To calculate that 


Now the equation is 
Expand the squared term:
Distribute the fraction through the parentheses:
Combine like terms:
For the graph below, match the graph b with one of the following equations:




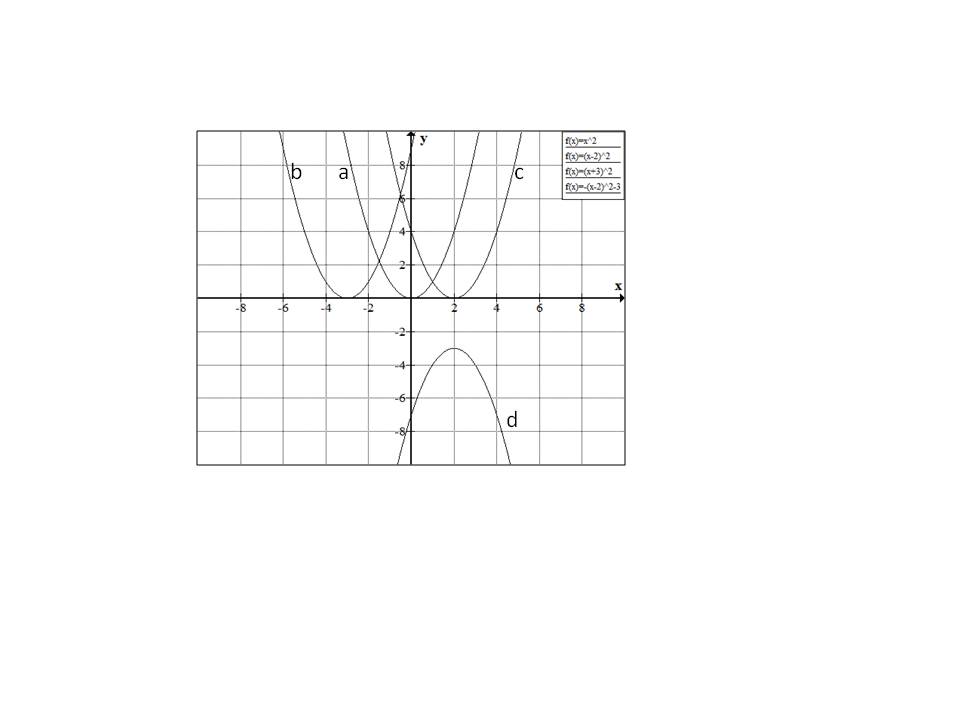




None of the above
Explanation
Starting with



Similarly 

Hence the correct answer is option 
What is the equation of a parabola with vertex 


Explanation
From the vertex, we know that the equation of the parabola will take the form 

To calculate that 


Now the equation is 
Expand the squared term:
Distribute the fraction through the parentheses:
Combine like terms:
Select the equation that best represents a linear function.
Explanation
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
We can add 
This equation is in slope-intercept form; thus, 
Select the equation that best represents a linear function.
Explanation
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
We can add 
This equation is in slope-intercept form; thus, 
Select the equation that best represents a linear function.
Explanation
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

For this equation, we can solve for 
First, we can subtract 
This equation is in slope-intercept form; thus, 
Select the equation that best represents a linear function.
Explanation
In order to determine if an equation defines a linear function, we want to make sure that the equation of the line is in slope-intercept form:
If we are unable to put an equation in this form, then the equation is not linear.
Let's take a look at our answer choices:
Notice that in this equation our 
Though this equation is not written in 

Again, though this equation is not written in 

This equation is in slope-intercept form; thus, 
For the graph below, match the graph b with one of the following equations:









None of the above
Explanation
Starting with



Similarly 

Hence the correct answer is option 









![\frac{\begin{array}[b]{r}y-2x=6\ +2x+2x\end{array}}{\\y=2x+6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963326/gif.latex)








![\frac{\begin{array}[b]{r}y+8x=24\ -8x-8x\end{array}}{\\y=-8x+24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963337/gif.latex)




















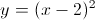










![\frac{\begin{array}[b]{r}y-3x=4x+3\ +3x+3x\ \ \ \ \ \end{array}}{\\y=7x+3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/963260/gif.latex)







