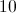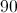8th Grade Math - Apply the Pythagorean Theorem to Determine Unknown Side Lengths in Right Triangles: CCSS.Math.Content.8.G.B.7

In a right triangle, two sides have length . Give the length of the hypotenuse in terms of .

$2\sqrt{2}t$

$\sqrt{2}t$

$2\sqrt{3}t$

$\sqrt{3}t$

Explanation

By the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Let hypotenuse and side length.

$c^2=s^2+s^2\Rightarrow c^2=(2t)^2+(2t)^2\Rightarrow c^2=8t^2\Rightarrow c=\sqrt{8t^2}=2\sqrt{2}t$

A right triangle has legs with the lengths and . Find the length of the hypotenuse.

$\sqrt{41}:cm$

$\sqrt{35}:cm$

Explanation

Use the Pythagorean Theorem to find the length of the hypotenuse.

$(\text{Hypotenuse})^2=(\text{leg 1})^2+(\text{leg 2})^2$

$\text{Hypotenuse}=\sqrt{4^2+5^2}=\sqrt{41}:cm$

Find the length of the hypotenuse of the following right triangle.

Explanation

Recall the Pythagorean Theorem, which is used to find the length of the hypotenuse.

For any triangle with leg lengths of and ,

$\text{Hypotenuse}^2=a^2+b^2$

Take the square root of both sides to find the length of the hypotenuse.

$\text{Hypotenuse}=\sqrt{a^2+b^2}$

Plug in the given values to find the length of the hypotenuse.

$\text{Hypotenuse}=\sqrt{12^2 + 5^2}=\sqrt{169}=13$

Find the length of the hypotenuse of the following right triangle.

$3\sqrt{41}$

$2\sqrt{41}$

$\sqrt{41}$

$4\sqrt{41}$

Explanation

Recall the Pythagorean Theorem, which is used to find the length of the hypotenuse.

For any triangle with leg lengths of and ,

$\text{Hypotenuse}^2=a^2+b^2$

Take the square root of both sides to find the length of the hypotenuse.

$\text{Hypotenuse}=\sqrt{a^2+b^2}$

Plug in the given values to find the length of the hypotenuse.

$\text{Hypotenuse}=\sqrt{15^2 + 12^2}=\sqrt{369}=3\sqrt{41}$

Calculate the length of the missing side of the provided triangle. Round the answer to the nearest whole number.

$20\textup{ cm}$

$21\textup{ cm}$

$19\textup{ cm}$

$18\textup{ cm}$

$17\textup{ cm}$

Explanation

The provided triangle is a right triangle. We know this because the angle marker in the left corner of the triangle indicates that the triangle possesses a right or $90^\circ$ angle. When a triangle includes a right angle, the triangle is said to be a "right triangle."

We can use the Pythagorean Theorem to help us solve this problem.

The Pythagorean Theorem states that for right triangles, the square of the hypotenuse is equal to the sum of the square of the other two sides. In other terms:

We can use the formula and substitute the known side lengths from the problem to solve for the missing side length:

$\sqrt{400}=\sqrt{c^2}$

If a right triangle has a base of and a height of , what is the length of the hypotenuse?

$\sqrt{90}$

Explanation

To solve this problem, we are going to use the Pythagorean Theorom, which states that $a^{2}+b^{2}=c^{2}$ .

We know that this particular right triangle has a base of , which can be substituted for , and a height of , which can be substituted for . If we rewrite the theorom using these numbers, we get:

$3^{2}+9^{2}=c^{2}$

Next, we evaluate the expoenents:

$3^{2}=9$

$9^{2}=81$

$9+81=c^{2}$

Then, $90=c^{2}$ .

To solve for , we must find the square root of . Since this is not a perfect square, our answer is simply $c=\sqrt{90}$ .

The legs of a right triangle are equal to 4 and 5. What is the length of the hypotenuse?

$\sqrt{41}$

Explanation

If the legs of a right triangle are 4 and 5, to find the hypotenuse, the following equation must be used to find the hypotenuse, in which c is equal to the hypotenuse:

$a^2{+b^{2}}=c^2$

$4^2{+5^{2}}=c^2$

$41=c^{2}$

$c={\sqrt{41}}$

Right_triangle

Refer to the above diagram, which depicts a right triangle. What is the value of ?

$3 \sqrt{ 13}$

$9\sqrt{3}$

$10\sqrt{2}$

Explanation

By the Pythagorean Theorem, which says . being the hypotenuse, or in this problem.

$x^{2} = 6^{2} + 9^{2}$

$x^{2} = 36 + 81$

$x^{2} = 117$

$x =\sqrt{ 117}$

Simply

$\sqrt{ 9} \cdot \sqrt{ 13}$

$3 \sqrt{ 13}$

Find the length of the hypotenuse of the following right triangle.

$\sqrt{26}$

$3\sqrt3$

$2\sqrt6$

Explanation

Recall the Pythagorean Theorem, which is used to find the length of the hypotenuse.

For any triangle with leg lengths of and ,

$\text{Hypotenuse}^2=a^2+b^2$

Take the square root of both sides to find the length of the hypotenuse.

$\text{Hypotenuse}=\sqrt{a^2+b^2}$

Plug in the given values to find the length of the hypotenuse.

$\text{Hypotenuse}=\sqrt{1^2 + 5^2}=\sqrt{26}$

Calculate the length of the missing side of the provided triangle. Round the answer to the nearest whole number.

$40\textup{ cm}$

$39\textup{ cm}$

$41\textup{ cm}$

$42\textup{ cm}$

$43\textup{ cm}$

Explanation

We can use the Pythagorean Theorem to help us solve this problem.

The Pythagorean Theorem states that for right triangles, the square of the hypotenuse is equal to the sum of the square of the other two sides. In other terms:

We can use the formula and substitute the known side lengths from the problem to solve for the missing side length: