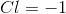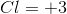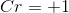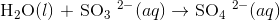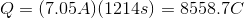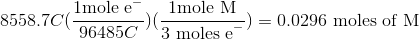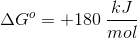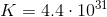Redox Reactions
Help Questions
AP Chemistry › Redox Reactions
Determine the oxidation number of each element in the compound
Explanation
The oxidation number of each element in the compound 
The oxidation number of chlorine is 
Because this is a neutral atom, the overall charge is 0. Therefore we can set
Therefore,
We can then solve for the oxidation number for
Balance the following redox reaction in acidic conditions:
Explanation
Start by writing the half reactions for the equation
All atoms except for O and H are already balanced, so we can go straight to balancing O and H atoms. First balance O atoms by adding H2O
Now balance H atoms with H+
Balance each half reaction's electrical charge with electrons
Now combine both half reactions to get the overall reaction. Be sure to cancel out electrons by multiplying the oxidation reaction by 5 and the reduction reaction by 2. This will give 10 e- on each side of the overall reaction so that they cancel out.
Overall Reaction:
Notice that we have H2O and H+ on both sides of the equation, so we need to simplify. Subtract the 5 H2O on the reactant side from the 8 H2O on the product side which leaves 3 H2O on the reactant side. Then subtract the 10 H+ on the product side from the 16 H+ on the reactant side which leave 6 H+ on the reactant side. Now we have the simplified overall reaction
Electrolysis of an unknown metal chloride, 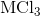
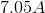
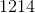
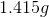
Titanium
Scandium
Chromium
Nickel
Explanation
Start by writing out the equation that illustrates the plating out of the metal:
Note the stoichiometric ratio for the moles of electrons to the moles of the metal.
Next, recall the following equation:
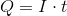



Plug in the given information to find 
Next, recall Faraday's law of electrolysis that equates Faraday's constant and the amount of electrons together to find the charge needed to deposit one mole of a particular substance.
Thus, we can set up the following to take the charge of the electrolysis through to figure out the number of moles unknown metal that was plated out.
Now, since we have the number of grams of the metal deposited, we can find the molar mass of the unknown metal.
The molar mass indicates that the metal must be titanium.
Consider the following redox reaction.
If 




Explanation
In this question, we're given an overall redox reaction as well as the relevant reduction potentials, and we're asked to solve for 
To begin with, we can show each of the individual half reactions to make it more clear.
For gold:
For bromine:
Note that the reduction potential for each of these half reactions is positive. This means that for both elements, their reduction is spontaneous. The more positive the voltage (or the less negative), the more spontaneous it is.
From the overall question given to us in the question stem, we see that bromine is not being reduced but, rather, it is being oxidized. Since oxidation is the reverse of reduction, the reduction potential maintains the same magnitude but the sign in front of it changes. Thus, the oxidation of bromine has a value of 
To find the overall 
One very important thing to note is that we did not need to multiply the reduction potential for either of the half reactions. Even though the reduction reaction for gold needs two stoichiometric equivalents, and bromine's oxidation needs three stoichiometric equivalents, the values of 



Consider the following redox reaction carried out in a voltaic cell.
If the reduction potential for 






Explanation
For this question, we're given a redox reaction occurring within a voltaic cell. We're also supplied with the reduction potentials for the elements in the reaction, and are asked to find the standard free energy change as well as the equilibrium constant of the reaction at a given temperature.
Recall that in a voltaic cell, the reaction does not consume energy but rather produces it. The anode is where oxidation occurs, while the cathode is where reduction takes place. Based on the reaction given to us in the question stem, the anode will consist of solid 
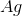




Knowing this, we can calculate 
Now that we have 
A couple things to note. The value for 

To find the value of 

Using 
Using 
As shown above, either method leads us to the same value for 
Electrolysis of an unknown metal chloride, 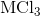
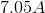
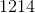
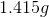
Titanium
Scandium
Chromium
Nickel
Explanation
Start by writing out the equation that illustrates the plating out of the metal:
Note the stoichiometric ratio for the moles of electrons to the moles of the metal.
Next, recall the following equation:
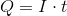



Plug in the given information to find 
Next, recall Faraday's law of electrolysis that equates Faraday's constant and the amount of electrons together to find the charge needed to deposit one mole of a particular substance.
Thus, we can set up the following to take the charge of the electrolysis through to figure out the number of moles unknown metal that was plated out.
Now, since we have the number of grams of the metal deposited, we can find the molar mass of the unknown metal.
The molar mass indicates that the metal must be titanium.
Consider the following redox reaction.
If 




Explanation
In this question, we're given an overall redox reaction as well as the relevant reduction potentials, and we're asked to solve for 
To begin with, we can show each of the individual half reactions to make it more clear.
For gold:
For bromine:
Note that the reduction potential for each of these half reactions is positive. This means that for both elements, their reduction is spontaneous. The more positive the voltage (or the less negative), the more spontaneous it is.
From the overall question given to us in the question stem, we see that bromine is not being reduced but, rather, it is being oxidized. Since oxidation is the reverse of reduction, the reduction potential maintains the same magnitude but the sign in front of it changes. Thus, the oxidation of bromine has a value of 
To find the overall 
One very important thing to note is that we did not need to multiply the reduction potential for either of the half reactions. Even though the reduction reaction for gold needs two stoichiometric equivalents, and bromine's oxidation needs three stoichiometric equivalents, the values of 



Consider the following redox reaction carried out in a voltaic cell.
If the reduction potential for 






Explanation
For this question, we're given a redox reaction occurring within a voltaic cell. We're also supplied with the reduction potentials for the elements in the reaction, and are asked to find the standard free energy change as well as the equilibrium constant of the reaction at a given temperature.
Recall that in a voltaic cell, the reaction does not consume energy but rather produces it. The anode is where oxidation occurs, while the cathode is where reduction takes place. Based on the reaction given to us in the question stem, the anode will consist of solid 
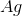




Knowing this, we can calculate 
Now that we have 
A couple things to note. The value for 

To find the value of 

Using 
Using 
As shown above, either method leads us to the same value for 
Determine the oxidation number of each element in the compound
Explanation
The oxidation number of each element in the compound 
The oxidation number of chlorine is 
Because this is a neutral atom, the overall charge is 0. Therefore we can set
Therefore,
We can then solve for the oxidation number for
Balance the following redox reaction in acidic conditions:
Explanation
Start by writing the half reactions for the equation
All atoms except for O and H are already balanced, so we can go straight to balancing O and H atoms. First balance O atoms by adding H2O
Now balance H atoms with H+
Balance each half reaction's electrical charge with electrons
Now combine both half reactions to get the overall reaction. Be sure to cancel out electrons by multiplying the oxidation reaction by 5 and the reduction reaction by 2. This will give 10 e- on each side of the overall reaction so that they cancel out.
Overall Reaction:
Notice that we have H2O and H+ on both sides of the equation, so we need to simplify. Subtract the 5 H2O on the reactant side from the 8 H2O on the product side which leaves 3 H2O on the reactant side. Then subtract the 10 H+ on the product side from the 16 H+ on the reactant side which leave 6 H+ on the reactant side. Now we have the simplified overall reaction