Solving Exponential Functions
Help Questions
College Algebra › Solving Exponential Functions
Solve the function:
Explanation
Change the base of the right side to base two.
Rewrite the equation.
With similar bases, set the powers equal.
Solve for x.
Subtract 
Divide by negative five on both sides.
The answer is:
Solve for 
Explanation
Since the bases of the exponents are the same (4), the exponents have to equal each other for the exponential equation to be true.
Solve:
Explanation
Change the right side to base three.
With similar bases, the exponents can be set equal.
Subtract one from both sides.
The answer is:
Solve for x:
Explanation
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:
Solve for x:
Explanation
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:
Solve for x:
Explanation
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:
Solve:
None of these
Explanation
add four to both sides:
divide both sides by four:
take the natural logarithm of both sides:
Divide both sides by three:
Solve for x:
Explanation
Step 1: We will take log of base 2 of both sides of the equation. The log base 2 will cancel out the base of the exponential term and just leave the exponent.
Step 2: We need to find the value of the right side. To find this number, we do the following:
Let 
Apply the rule: Raise the base of the log to the power (the solution), and this expression is equal to the value next to the base of the exponent.
So:
If 
So, 
Since the bases of the two exponential functions are the same, then the exponents of both exponential functions must also be the same.
The answer is:
Give the solution set for the exponential equation shown below for the following cases:
Case 1,
Case 2
Case 1:
All real values of 
Case 2:
Case 1:
There are no solutions,
Case 2:
Case 1:
Case 2:
Case 1:
Case 2:
There is not enough information to find 

Case 1:
All real values of 
Case 2:
All real values of 
Explanation
Case 1,
This is true for all real values of 
Case 2
Take the natural logarithm of both sides (note that we could use any logarithm but it's convenient to just choose the natural logarithm).
Use the rule for pulling out exponents 
Note that if you were to divide out by 



Expand with the distributive property,
Collect and isolate terms with 
Factor out 


What's remarkable about this solution is that it was obtained without specifying any value for 


Solve for x:
Explanation
In order to solve for x when it is in the exponent, we need to make the bases on either side of the equation look the same. In order to do this, factor the larger number until it looks like the smaller one. For this problem that looks as follows:
Factor the larger number:
Now substitute in the factored number:
Since the bases are now the same:


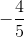

















































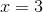

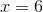


















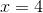























![\ln\left(a^{10x-1} \right ) = \ln\left[b^{10x-1}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736239/gif.latex)



![10x[\ln(a)-\ln(b)]=\ln(a)-\ln(b)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/736247/gif.latex)











