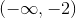Solving Equations and Inequallities
Help Questions
College Algebra › Solving Equations and Inequallities
Solve:
Explanation
We need to set up two equations since we are dealing with absolute value
We solve for 
Solve:
Explanation
We need to set up two equations since we are dealing with absolute value
We solve for 
Express the following linear inequality in interval notation.
Explanation
Upon solving for x, we find that x is larger than -2. The left-hand term of the interval is -2 since it is the lower bound for our set, and it has a parenthesis around it because it is not included in our set (-2 is not greater than -2). The right-hand term of the interval is positive infinity because any number larger than -2 is in the set. There is always a parenthesis around infinity or negative infinity.
Express the following linear inequality in interval notation.
Explanation
Upon solving for x, we find that x is larger than -2. The left-hand term of the interval is -2 since it is the lower bound for our set, and it has a parenthesis around it because it is not included in our set (-2 is not greater than -2). The right-hand term of the interval is positive infinity because any number larger than -2 is in the set. There is always a parenthesis around infinity or negative infinity.
Solve the inequality:
Explanation
To solve for 
Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.
Solve the inequality:
Explanation
To solve for 
Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.
Solve:
Explanation
Move 
Simplify:
Divide by the coefficient, the number in front of x.
Reduce:
Solve:
Explanation
We need to set up two equations since we are dealing with absolute value
We solve for 
Solve:
Explanation
Move 
Simplify:
Divide by the coefficient, the number in front of x.
Reduce:
Solve:
Explanation
We need to set up two equations since we are dealing with absolute value
We solve for 

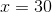






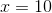




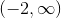
![\left [ -2,\infty \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1009903/gif.latex)