Equations
Help Questions
AP Calculus AB › Equations
Write the correct expression to find the area of 
![[-2,2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/328385/gif.latex)
Explanation
This is a tricky question.
If we chose 


The correct method is to split this interval into 2 separate integrations: One from ![[-2,0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/328389/gif.latex)
![[0,2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/328390/gif.latex)
From interval ![[-2,0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/328391/gif.latex)



From interval ![[0,2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/328395/gif.latex)



Set up the integral.
Solve the following integral, where a and b are constants:
Explanation
Keeping in mind that a and b are only constants, the integral is equal to
and was found using the following rule:
Take the indefinite integral of
Indefinite integral does not exist
Explanation
First, foil the integral so it is easier to manage.
then perform the indefinite integral the normal way you would do
Evaluate the definite integral within the interval
Explanation
In order to solve this problem we must remember that:
In this case we have:
Our first step is to integrate:
We then arrive to our solution by plugging in our values
What is the equation of the tangent line at x = 15 for f(x) = x4 + 5x2 + 44x – 3?
y = 55x + 13382
y = 2848x + 34
y = 153103x – 13694
None of the other answers
y = 13694x – 153003
Explanation
First we must solve for the general derivative of f(x) = f(x) = x4 + 5x2 + 44x – 3.
f'(x) = 4x3 + 10x + 44
Now, the slope of the tangent line for f(15) is equal to f'(15):
f'(15) = 4(15)3 + 10 *15 + 44 = 13694.
To find the tangent line, we need at least one point on the line. To find this, we can use f(15) to get the y value of the point of tangency, which will suffice for our use:
f(15) = 154 + 5(15)2 + 44 * 15 – 3 = 50625 + 1125 + 660 – 3 = 52407
Now, using the point-slope form of the line, we get:
y - 52407 = 13694 * (x – 15)
Simplify:
y – 52407 = 13694x – 205410
y = 13694x – 153003
Given the one-to-one equation f(x)=3x+1, the inverse function f-1(y)=
3x-1
(x-1)/3
(y+1)/3
(y-1)/3
undefined
Explanation
Before we solve the problem by computation, let's look at the answer choices and see if we can eliminate any answer choices. We know that an inverse function must exist because f(x) is one-to-one, so we can eliminate the answer choice "undefined." Next, we know that the inverse function has to be in terms of y, so we can eliminate the two answer choices with an "x."
Now we can look at the two remaining answer choices. Let y=f(x) and solve for x to find the inverse.
So f(x)=y=3x+1. Solve for x.
x=(y-1)/3
Therefore our answer is (y-1)/3.
Explanation
When integrating, remember to add one to the exponent and then put that result on the denominator: 

Evaluate the following integral:
Explanation
To integrate, we must make the following subsitution:
We used the following rule to derivate:
Now, after rearranging, we get the following integral:
and after integrating we get
We used the following rule to integrate:
To finish, we plug our x term back in place of u:
Evaluate the following indefinite integral:
Explanation
To evaluate the integral the integral, use the inverse power rule:
Applying that rule to this problem gives us the following for the first term:
The following for the second term:
And the following for the third term:
We can combine these terms and add our "C" to get the final answer:
Explanation
To integrate this expression, you must use "u" substitution. The expression you assign to "u" is usually the expression with the higher exponent; in this case, 

The derivative of our u expression is


Now we can fully plug into our integral expression so we can integrate. You can rewrite the expression so it looks like this:

Everything in the u terms fully replaced everything in the original expression. Now, we can integrate. When we integrate 

Since it's an indefinite expression, we must add +C at the end. The last step is to sub back in the expression that "u" represents.
Therefore, our final answer is















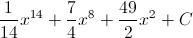















![\left [ 2\sqrt{9}+(9)^{3}-4(9) \right ]-\left [ 2\sqrt{4}+(4)^{3}-4(4) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/279464/gif.latex)

































