Parametric Curves
Help Questions
AP Calculus BC › Parametric Curves
Find the equation of the line passing through the two points, given in parametric form:
Explanation
To find the equation of the line passing through these two points, we must first find the vector between them:
This was done by finding the difference between the x, y, and z components for the vectors. (This can be done in either order, it doesn't matter.)
Now, pick a point to be used in the equation of the line, as the initial point. We write the equation of line as follows:
The choice of initial point is arbitrary.
Find the coordinates of the curve function
when
Explanation
To find the coordinates, we evaluate the curve function for
As such,
Find the coordinates of the curve function
when
Explanation
To find the coordinates, we evaluate the curve function for
As such,
Find the coordinate of the parametric curve when

Explanation
To find the coordinates of the parametric curve we plug in for

As such the coordinates are
Find the length of the parametric curve described by
from 

None of the other answers
Explanation
There are several ways to solve this problem, but the most effective would be to notice that we can derive the following-
Hence
Therefore our curve is a circle of radius 






Alternatively, we could've found the length using the formula

Find the coordinates of the curve function
when 
Explanation
To find the coordinates, we set 
We get
and thus
Write the parametric equations of the line that passes through the points 

Explanation
First, you must find the vector that is parallel to the line.
This vector is

From the points we were given, this becomes

To form the parametric equations, we need to pick a point that lies on the line we want.
The point 
The vector form of the line is from the following equation

We then rewrite each expression in terms of the variables x, y, and z.
Evaluate the line integral 



Explanation
Evaluate the line integral 



Define the Parametric Equations to Represent
The points given lie on the line 




_________________________________________________________________
The line integral of a function 





Where 


______________________________________________________________
Write the vector 
Differentiate,
The absolute value (magnitude) of this vector is:
Write the function 

Insert everything into Equation (1) noting that the limits of integration will be 


















































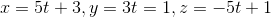
















![=\frac{\sqrt{41}}{4}\left[\frac{5}{8}t^2+\frac{1}{\pi}\sin(\pi t) \right ]_{t=0}^{t=4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933661/gif.latex)
![=\frac{\sqrt{41}}{4}\left[\frac{5}{8}(16)+\frac{1}{\pi }\sin(4 \pi) -0-\frac{1}{\pi}\sin(0)\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/933662/gif.latex)
