Plane Geometry
Help Questions
Geometry › Plane Geometry
Know that in a Major League Baseball infield the distance between home plate and first base is 90 feet and the infield is a perfect square.
What is the area of a Major League Baseball infield?
Explanation
Because the infield is a square, the distance between each set of bases is 90 feet.
To find the area of a square you multiply the length by the width.
In this case


In the figure above, 



Explanation
Assigning the length of ED the value of x, the value of AE will be 3_x_. That makes the entire side AD equal to 4_x_. Since the figure is a square, all four sides will be equal to 4_x_. Also, since the figure is a square, then angle A of triangle ABE is a right angle. That gives triangle ABE sides of 3_x_, 4_x_ and 10. Using the Pythagorean theorem:
(3_x_)2 + (4_x_)2 = 102
9_x_2 + 16_x_2 = 100
25_x_2 = 100
_x_2 = 4
x = 2
With x = 2, each side of the square is 4_x_, or 8. The area of a square is length times width. In this case, that's 8 * 8, which is 64.
Find the perimeter.

Explanation
How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 





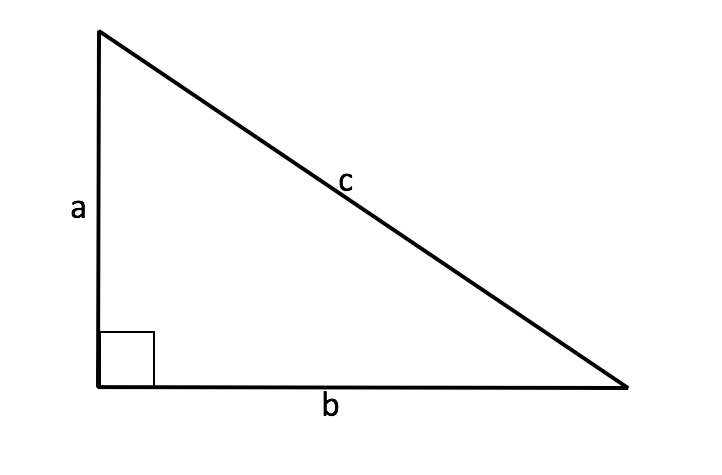
If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
Recall how to find the perimeter of a triangle:
The given triangle has 
Recall the Pythagorean theorem:

Since we are finding the length of the hypotenuse, 
Plug in the values of 

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to 
Find the perimeter.

Explanation
How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
Recall how to find the perimeter of a triangle:
The given triangle has 
Recall the Pythagorean theorem:

Since we are finding the length of the hypotenuse, 
Plug in the values of 

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to 
Find the perimeter.

Explanation
How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

In order to find the perimeter, we must first find the length of the hypotenuse of the right triangle.
Use Pythagorean's theorem to find the length of the hypotenuse:
Plug in the values of the lengths of the legs of the given triangle.
Now, recall how to find the perimeter of a triangle:
Plug in all the values of the sides of the triangle to find the perimeter.
Make sure to round to 
Find the perimeter.

Explanation
How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.

In order to find the perimeter, we must first find the length of the hypotenuse of the right triangle.
Use Pythagorean's theorem to find the length of the hypotenuse:
Plug in the values of the lengths of the legs of the given triangle.
Now, recall how to find the perimeter of a triangle:
Plug in all the values of the sides of the triangle to find the perimeter.
Make sure to round to 
Find the area of a circle that has a radius of 
Explanation
Use the following formula to find the area of a circle:
For the circle in question, plug in the given radius to find the area.
We know the radius is 

Recall that when a square root is squared you are left with the number under the square root sign. This happens because when you square a number you are multiplying it by itself. In our case this is,

From here we can use the property of multiplication and radicals to rewrite our expression as follows,
and when there are two numbers that are the same under a square root sign you bring out one and the other number and square root sign go away.
Find the perimeter.

Explanation
How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
Recall how to find the perimeter of a triangle:
The given triangle has 
Recall the Pythagorean theorem:
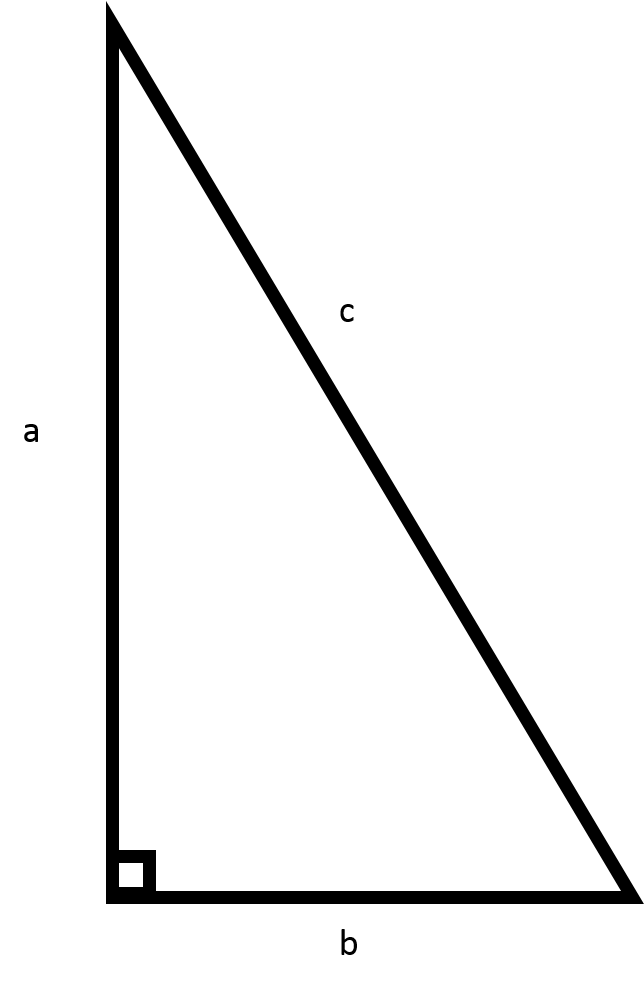
Since we are finding the length of side 
Plug in the values of 

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to 
In order to get to work, Jeff leaves home and drives 4 miles due north, then 3 miles due east, followed by 6 miles due north and, finally, 7 miles due east. What is the straight line distance from Jeff’s work to his home?
2√5
11
10√2
15
6√2
Explanation
Jeff drives a total of 10 miles north and 10 miles east. Using the Pythagorean theorem (a2+b2=c2), the direct route from Jeff’s home to his work can be calculated. 102+102=c2. 200=c2. √200=c. √100√2=c. 10√2=c
If the diameter of the circle below is 

Explanation

From the given figure, you should notice that the base of the triangle is the same as the diameter of the circle.
In order to find the area of the shaded region, we will first need to find the area of the circle and the area of the triangle.
Recall how to find the area of a circle:
Now recall the relationship between the radius and the diameter.
Plug in the value of the diameter to find the value of the radius.
Now, plug in the value of the radius in to find the area of the circle.
Next, recall how to find the area of a triangle.
The height is already given by the question, and remember that the base is the same as the diameter of the circle.
Plug in these values to find the area of the triangle.
We are now ready to find the area of the shaded region.
Remember to round to 






























































































