How to find the length of the side of a 45/45/90 right isosceles triangle
Help Questions
Geometry › How to find the length of the side of a 45/45/90 right isosceles triangle
Angle 


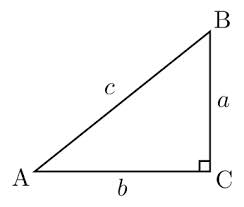
Explanation
Since we know two of the three angles in this triangle, we can calculate the third, 
Therefore this is a 45/45/90 right triangle. Remember that 45/45/90 right triangles are have a leg:leg:hypotenuse ratio of 1:1:
We know the hypotenuse, 


To make this look like one of the answer choies, rationalize the denominator by muliplying the fraction by 
The following image is not to scale.
Find the length of one of the legs of the right triangle.
Explanation
Because of the tick marks on both legs, we can determine that this right triangle is a 45/45/90 triangle. Because the length of both legs are the same, this means that the angle opposite of each leg is also the same.
45/45/90 triangles are special, just like 30/60/90 triangles. Solving for one of the leg lengths can be determined easily through remembering the following:
Using this and the 7ft, we can solve for "s" which will provide us with the leg length.

The perimeter of a 45-45-90 triangle is 100 inches. To the nearest tenth of an inch, what is the length of each leg?
Explanation
Let 

Therefore,
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Explanation

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.

Explanation
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Explanation

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
If the hypotenuse of a right isosceles triangle is 
Explanation
A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
In the figure, a right isosceles triangle is placed in a rectangle. What is the area of the shaded region?

Explanation

In order to find the area of the shaded region, we need to first find the areas of the triangle and the rectangle.
First, recall how to find the area of a triangle.
In the figure, we are given the triangle’s hypotenuse, which is also the width of the rectangle. We can then use this information and the Pythagorean theorem to find the length of the sides of the triangle.
Now, because this is a right isosceles triangle,
We can then make the following substitution:
Therefore:
Substitute in the value of the hypotenuse to find the length of the base:
Now, substitute this number in to find the area of the triangle.
Next, recall how to find the area of the rectangle:
Substitute in the given information from the question to find the area.
Now that we have the areas of both the rectangle and the triangle, we can find the area of the shaded region.
Solve.
If the hypotenuse of a right isosceles triangle is 
Explanation
A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.
Reduce.
If the hypotenuse of a right isosceles triangle is 
Explanation
A right isosceles triangle is also a 

To find the length of a side, we will need to use the Pythagorean Theorem:
Since this is an isosceles triangle,
The Pythagorean Theorem can then be rewritten as the following:
Since we are trying to find the length of a side of this triangle, solve for 
Simplify.
Multiply the fraction by one in the form of 
Solve.
Now, substitute in the length of the hypotenuse in for 
Simplify.

















































































































