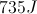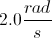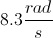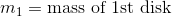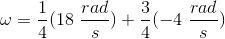Mechanics Exam
Help Questions
AP Physics C: Electricity and Magnetism › Mechanics Exam
Which of the following could be used as units of impulse?
Explanation
Relevant equations:
Impulse is defined as change in momentum, so has the same units as momentum. These units can easily be found using the given equations.
A 25kg child climbs up a tree. How much work is required for him to climb up this tree to a height of three meters?
Explanation
The forces acting on the child are the force of gravity and the upward force provided by the child himself. Choosing the upward direction as positive, Newton's second law applied to the child gives the following equation.
To calculate the work done by the child to bring himself three meters up the tree, we use the work equation below.
An object is pushed across a rough surface with a force of 53N. The rough surface exerts a frictional force of 3.47N on the object. If the object is pushed 7.9m, how much work is done on the object?
Explanation
The defintion of work is:
The net force on this object is:
We can calculate this term using the given values:
The distance is given. Substituting these values:
Starting from rest, a skateboarder travels down a 25o incline that's 22m long. Using conservation of energy, calculate the skateboarder's speed when he reaches the bottom. Ignore friction.
Explanation
Conservation of energy states that 
The skateboarder starts from rest; thus, 



Solve for v.
Using trigonometry, 
A 



What is the mass of the block?
Explanation
This problem is a conservation of momentum problem. When doing these types of problems, the equation to jump to is:
It is given to us that 











With all this information given, the only unknown is 
Plugging everything in, we get:
An object is pushed across a rough surface with a force of 53N. The rough surface exerts a frictional force of 3.47N on the object. If the object is pushed 7.9m, how much work is done on the object?
Explanation
The defintion of work is:
The net force on this object is:
We can calculate this term using the given values:
The distance is given. Substituting these values:
A 

I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
I and III
I and II
I, II, and III
I only
II only
Explanation
Relevant equations:
Choice I is true because 




Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon 
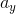


A 25kg child climbs up a tree. How much work is required for him to climb up this tree to a height of three meters?
Explanation
The forces acting on the child are the force of gravity and the upward force provided by the child himself. Choosing the upward direction as positive, Newton's second law applied to the child gives the following equation.
To calculate the work done by the child to bring himself three meters up the tree, we use the work equation below.
A 25kg child climbs up a tree. How much work is required for him to climb up this tree to a height of three meters?
Explanation
The forces acting on the child are the force of gravity and the upward force provided by the child himself. Choosing the upward direction as positive, Newton's second law applied to the child gives the following equation.
To calculate the work done by the child to bring himself three meters up the tree, we use the work equation below.
Two solid cylinderical disks have equal radii. The first disk is spinning clockwise at 

Explanation
For the first disk, we have the information below.
For the second disk, we have the information below.
(The minus sign indicates counterclockwise while the positive indicates clockwise.)
To do this problem, we use conservation of angular momentum. Before the disks are put in contact, the initial total angular momentum is given by the equation below.
It is just the sum of the angular momentums of each disk. When the disks are combined together, then final angular momentum can be found by the following equation.
Set this equal to the initial angular momentum.
Simplify and solve for